\(\newcommand{\E}{\\[3pt]}\) \(\newcommand{\DE}{\\[6pt]}\) \(\newcommand{\TE}{\\[9pt]}\) \(\newcommand{\QE}{\\[12pt]}\) \(\newcommand{\eps}{\varepsilon}\) \(\newcommand{\beps}{\boldsymbol\eps}\) \(\newcommand{\bsig}{\boldsymbol\sigma}\) \(\newcommand{\dbdot}{\,\colon\!}\) \(\newcommand{\hint}{\displaystyle\int}\) \(\newcommand{\hsum}{\displaystyle\sum}\) \(\newcommand{\alert}[1]{{\color{pdcolor9}#1}}\) \(\newcommand{\gives}{\quad\Rightarrow\quad}\) \(\newcommand{\ud}{\mathrm{d}}\) \(\newcommand{\uf}{\mathrm{f}}\) \(\newcommand{\bff}{\mathbf{f}}\) \(\newcommand{\ba}{\mathbf{a}}\) \(\newcommand{\bb}{\mathbf{b}}\) \(\newcommand{\bc}{\mathbf{c}}\) \(\newcommand{\bh}{\mathbf{h}}\) \(\newcommand{\bn}{\mathbf{n}}\) \(\newcommand{\bq}{\mathbf{q}}\) \(\newcommand{\bt}{\mathbf{t}}\) \(\newcommand{\bu}{\mathbf{u}}\) \(\newcommand{\bv}{\mathbf{v}}\) \(\newcommand{\bw}{\mathbf{w}}\) \(\newcommand{\bx}{\mathbf{x}}\) \(\newcommand{\bB}{\mathbf{B}}\) \(\newcommand{\bD}{\mathbf{D}}\) \(\newcommand{\bJ}{\mathbf{J}}\) \(\newcommand{\bK}{\mathbf{K}}\) \(\newcommand{\bM}{\mathbf{M}}\) \(\newcommand{\bN}{\mathbf{N}}\) \(\newcommand{\bP}{\mathbf{P}}\) \(\newcommand{\bzero}{\mathbf{0}}\) \(\newcommand{\pder}[2]{\frac{\partial #1}{\partial #2}}\) \(\newcommand{\dder}[2]{\frac{\ud #1}{\ud #2}}\) \(\newcommand{\pders}[3]{\frac{\partial^2 #1}{\partial #2 \partial #3}}\) \(\newcommand{\lder}[2]{{\ud #1}/{\ud #2}}\) \(\newcommand{\lpder}[2]{{\partial #1}/{\partial #2}}\) \(\newcommand{\lpders}[3]{{\partial^2 #1}/{\partial #2 \partial #3}}\) \(\newcommand{\hfrac}[2]{\displaystyle\frac{#1}{#2}}\) \(\newcommand{\lfrac}[2]{{#1}/{#2}}\) \(\newcommand{\hpder}[2]{\displaystyle\frac{\partial #1}{\partial #2}}\) \(\newcommand{\myVec}[1]{\left\{ \begin{matrix} #1 \end{matrix} \right\}}\) \(\newcommand{\myMat}[1]{\left[ \begin{matrix} #1 \end{matrix} \right]}\) \(\newcommand{\sym}{\ensuremath{_\mathrm{s}}}\) \(\newcommand{\dg}{\ensuremath{^\circ}}\) \(\newcommand{\mbf}[1]{\mathbf{#1}}\) \(\newcommand{\mrm}[1]{\mathrm{#1}}\) \(\newcommand{\bs}[1]{\boldsymbol{#1}}\) \(\newcommand{\T}{^\mathrm{T}}\) \(\newcommand{\dOmega}{\,\mathrm{d}\Omega}\) \(\newcommand{\dGamma}{\,\mathrm{d}\Gamma}\) \(\newcommand{\us}{\mathrm{s}}\) \(\newcommand{\old}{_0}\) \(\newcommand{\new}{_1}\)
\(\newcommand{cA}[1]{\textcolor[RGB]{1,113,136}{#1}}\) \(\newcommand{cB}[1]{\textcolor[RGB]{195,49,47}{#1}}\) \(\newcommand{cC}[1]{\textcolor[RGB]{0,102,162}{#1}}\) \(\newcommand{cD}[1]{\textcolor[RGB]{0,183,211}{#1}}\) \(\newcommand{cE}[1]{\textcolor[RGB]{0,163,144}{#1}}\) \(\newcommand{cF}[1]{\textcolor[RGB]{97,164,180}{#1}}\) \(\newcommand{cG}[1]{\textcolor[RGB]{130,215,198}{#1}}\) \(\newcommand{cH}[1]{\textcolor[RGB]{153,210,140}{#1}}\) \(\newcommand{cI}[1]{\textcolor[RGB]{235,114,70}{#1}}\) \(\newcommand{cJ}[1]{\textcolor[RGB]{241,190,62}{#1}}\) \(\newcommand{cK}[1]{\textcolor[RGB]{231,41,138}{#1}}\)
5.3. Incremental-iterative algorithms#
We have seen that in nonlinear FEM problems the internal force \(\bff_\mrm{int}\) is a nonlinear function of \(\ba\). We have also seen that solving for equilibrium means finding \(\ba\) such that \(\bff_\mrm{int}(\ba)=\bff_\mrm{ext}\). Since this is a nonlinear equation that will be solved iteratively, it is useful to recast it as a residual vector:
which we will be trying to bring to zero. With this we recast the equilibrium problem as finding the root of \(\mbf{r}\) for a given \(\bff_\mrm{ext}\).
Newton-Raphson method revisited#
Newton’s method is a classic algorithm for finding roots of nonlinear functions. We briefly recap it here before going back to equilibrlium. Let \(f(x)\) be an arbitrary scalar nonlinear function, an example of which is shown below (left plot):
Fig. 5.2 The Newton-Raphson method. Left: as a root-finding algorithm for an arbitrary function \(f(x)\); Right: recast as a solver for \(\bff_\mrm{int}=\bff_\mrm{ext}\).#
The goal of Newton’s method is to solve the equation \(f(x)=0\) for \(x\). To do this we start with an initial guess \(x\old\) and construct a linear approximation of \(f(x)\):
for which it is easy to compute the root \(\widetilde{f}(x)=0\). We can therefore reach a new approximation \(x\new\) for the root:
with the idea being that if \(\widetilde{f}(x)\) is a fair approximation of \(f(x)\), we start from a good initial guess, and repeat this operation enough times we can get arbitrarily close to the actual root.
Newton-Raphson for FEM#
In the example above we have applied Newton’s method for a scalar function of a single variable. Actually, the procedure generalizes trivially to vectors, and we can directly apply it to solve Eq. (5.12). For a fixed \(\bff_\mrm{ext}\) and starting from an initial guess \(\ba\old\), we can define our linearized residual as:
where \(\mbf{r}\old = \mbf{r}(\ba\old)\). Recalling our discussion \(\bff_\mrm{int}\) in the previous page, we can directly write the derivative we need above:
Finally, we use the resulting linearization to compute a new guess for \(\ba\):
with which we can repeat this process until \(\mbf{r}\) is close enough to zero.
Coding FEM
Just as for linear problems, the value of \(\ba\new\) above is not actually computed by inverting \(\bK\). We instead solve the linearized system of equations \(\bK\ba=\mbf{r}\old\). Refer back to the discussion in Linear algebra for more details on how this is done.
The Newton-Raphson method is numerical in nature and therefore needs a stopping criterium (i.e. the residual can get arbitrarily close to zero but never exactly zero). It is usual to look at the norm \(|\mbf{r}|\), or a scaled version of it. It is also possible to look at \(|\Delta\ba|\) of subsequent iterations and stop when \(\ba\) is not changing significantly. Metrics involving both \(\mbf{r}\) and \(\Delta\ba\) can also be used. The following animation illustrates the complete procedure:
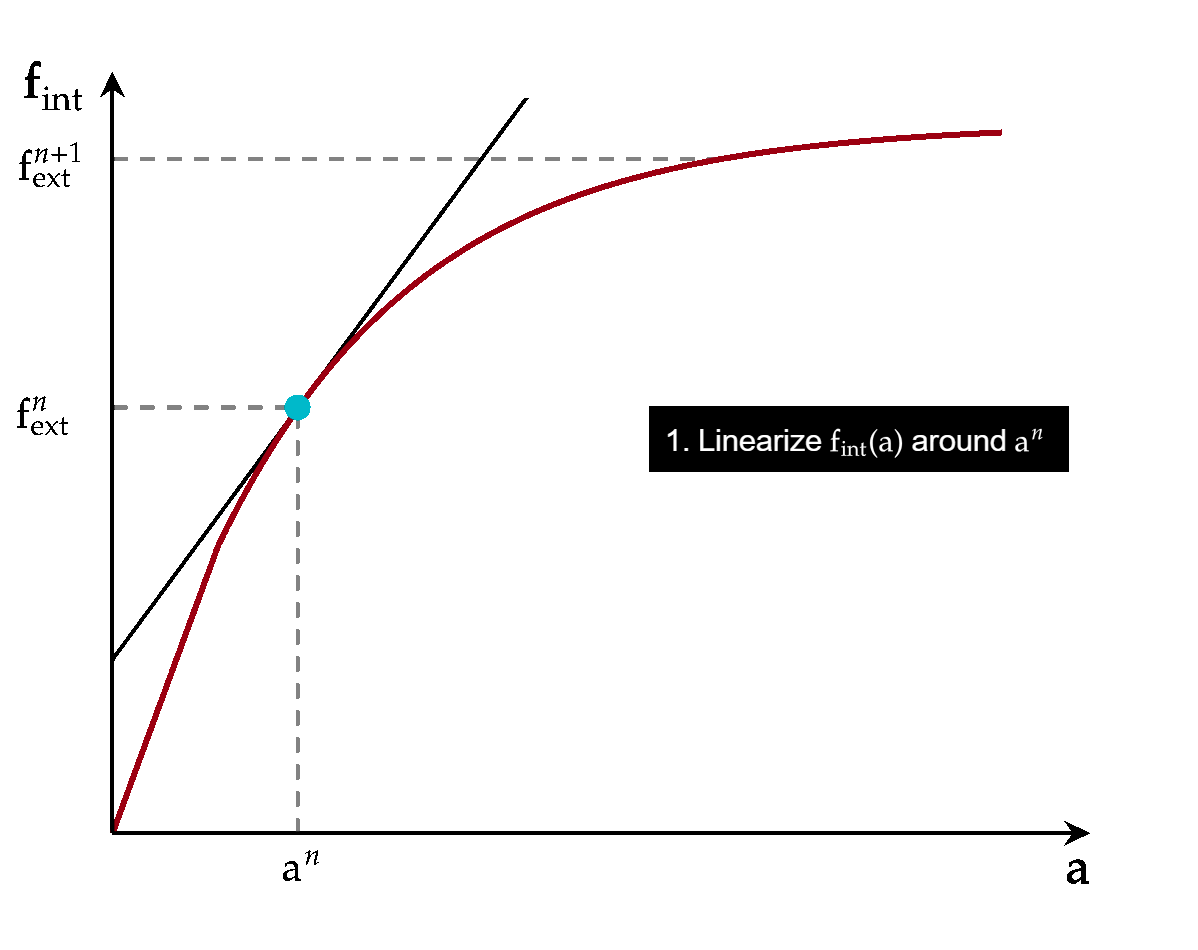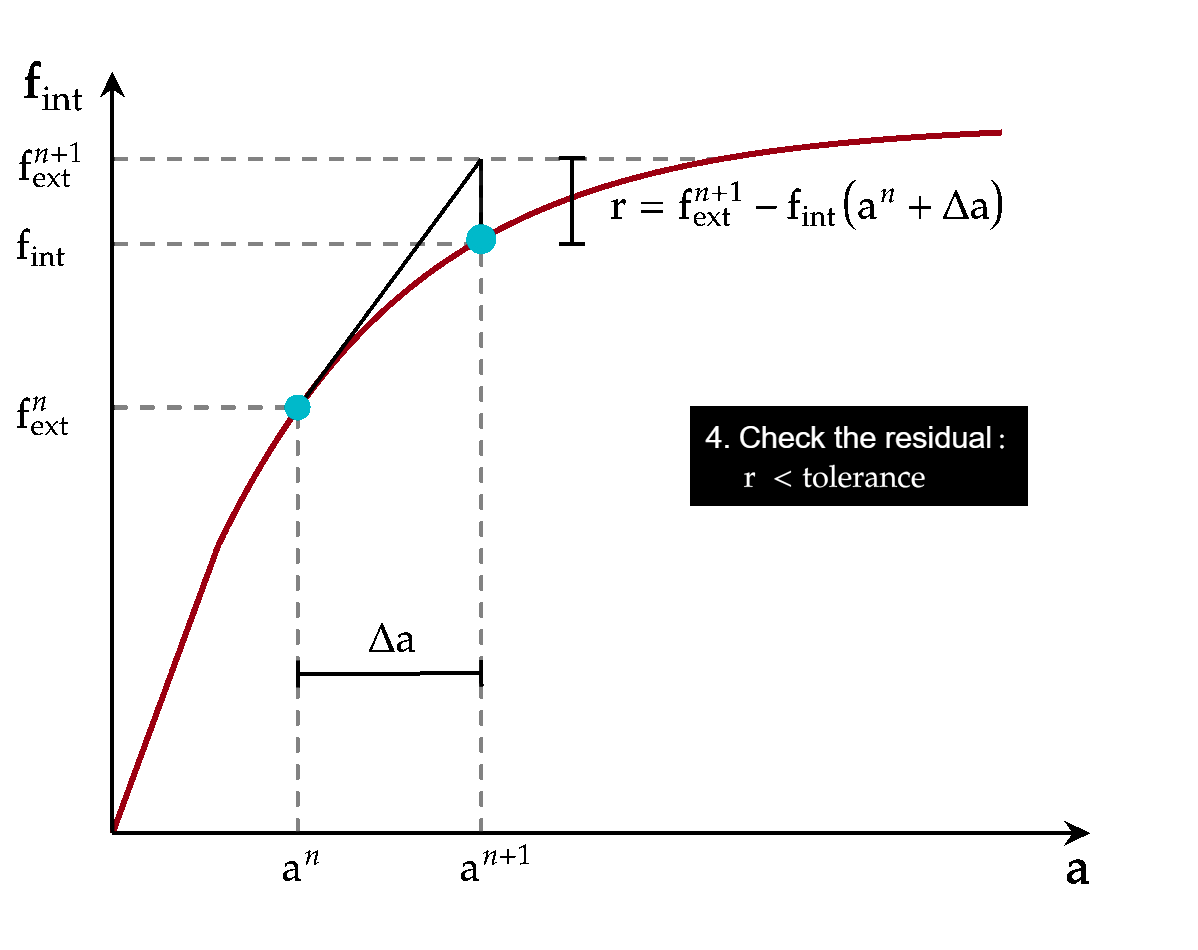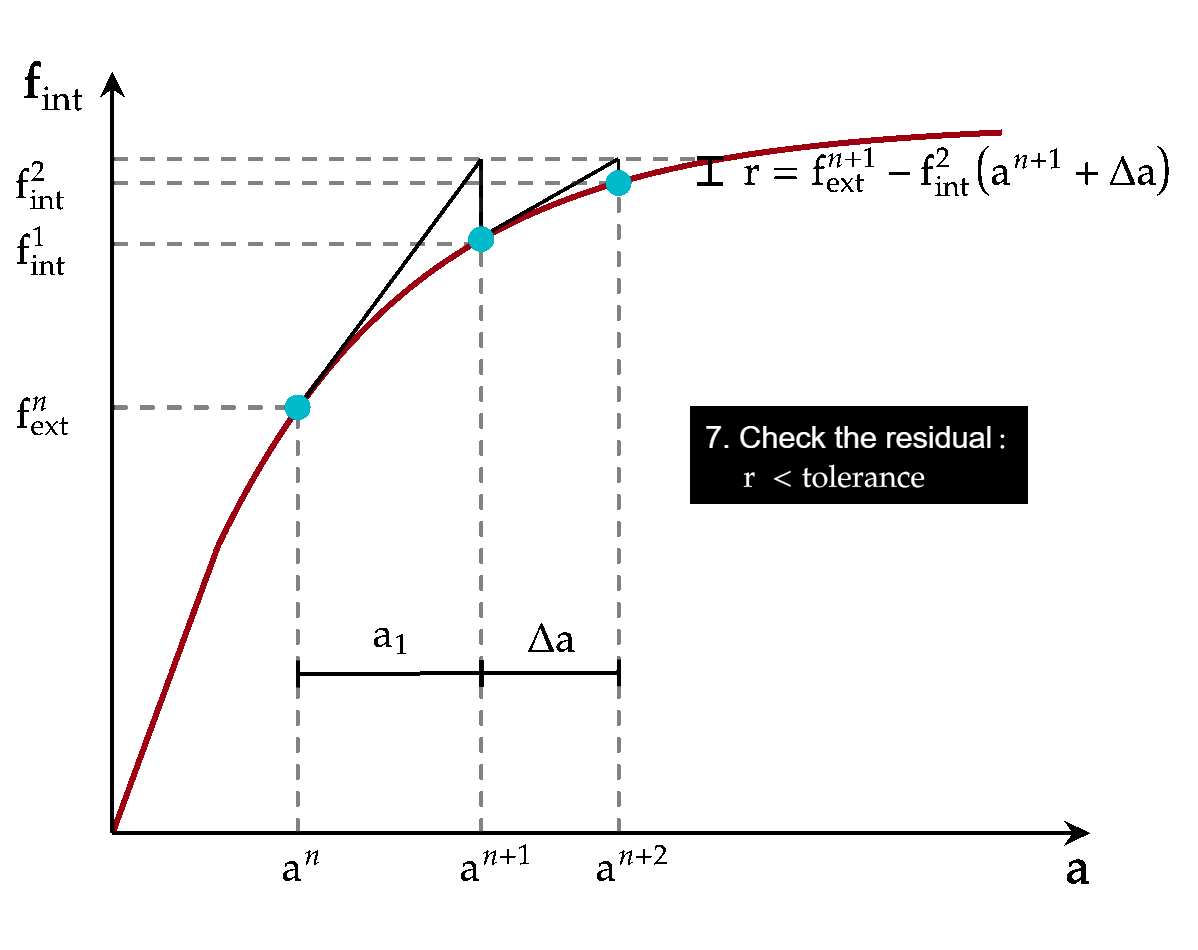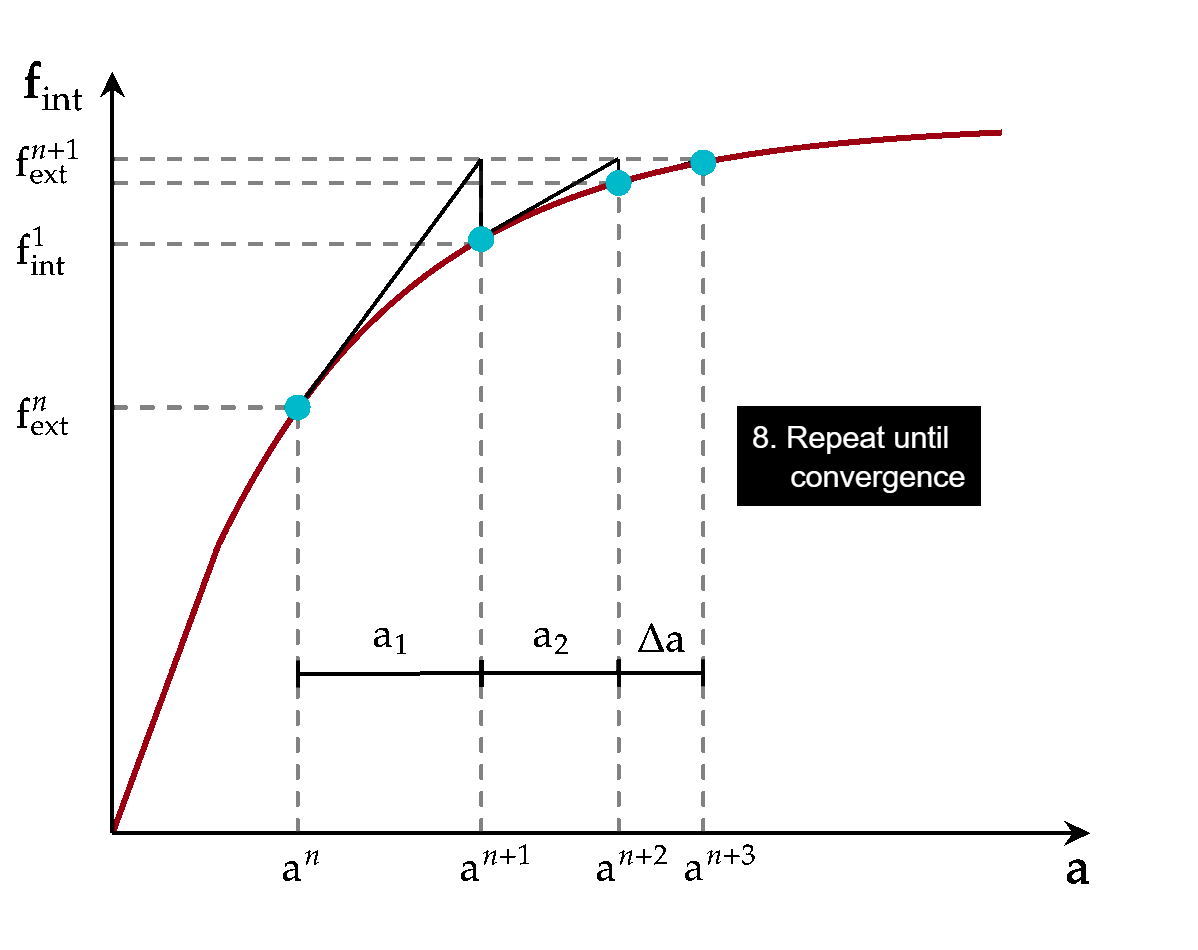
Fig. 5.3 Iterations in the Newton-Raphson method for an equilibrium problem#
Finally, it is worth noting that the efficiency of the method relies on a good initial guess for \(\ba\). The further away we are to the actual equilibrium point the lower the quality of the linear approximation of Eq. (5.15). This is one of the reasons why we are interested in gradually tracing the equilibrium path instead of jumping straight to the final value of \(\bff_\mrm{ext}\) or to a final displacement of interest.
Path-following techniques#
We can use Newton’s method in the same form as above to formulate different equilibrium path following strategies, the most straightforward of which is load control. In the discussion above, \(\bff_\mrm{ext}\) had been considered known and fixed. In load control the goal is to gradually increase \(\bff_\mrm{ext}\) in a number of increments. Within each increment, we solve for equilibrium in an iterative way using Newton’s method. It is therefore a so-called incremental-iterative approach, the main steps of which are shown below:
Load control
Require: Nonlinear relation \(\bff_\mrm{int}(\ba)\) with \(\bK(\ba) = \pder{\bff_\mrm{int}}{\ba}\)
Initialize: \(n=0\), \(\ba^0=\mbf{0}\)
while \(n<\text{number of time steps}\):
Get new external force vector: \(\bff_\mrm{ext}^{n+1}\)
Initialize new solution at old one: \(\ba^{n+1} = \ba^n\)
Compute internal force and stiffness: \(\bff_\mrm{int}^{n+1}(\ba^{n+1})\), \(\bK^{n+1}(\ba^{n+1})\)
Evaluate residual: \(\mbf{r} = \bff_\mrm{ext}^{n+1} - \bff_\mrm{int}^{n+1}\)
while \(|\mbf{r}| > \text{tolerance}\):
Solve linear system of equations: \(\bK^{n+1} \Delta\ba = \mbf{r}\)
Update solution: \(\ba^{n+1} = \ba^{n+1} + \Delta\ba\)
Compute internal force and stiffness: \(\bff_\mrm{int}^{n+1}(\ba^{n+1})\), \(\bK^{n+1}(\ba^{n+1})\)
Evaluate residual: \(\mbf{r} = \bff_\mrm{ext}^{n+1} - \bff_\mrm{int}^{n+1}\)
Go to the next time step: \(n=n+1\)
Return: Set of internal forces and displacements (equilibrium path)
Load control is straightforward and suitable to a number of real-world applications. Nevertheless, it can lead to convergence issues and not be able to trace a full equilibrium path depending on the shape of the path. One example of such a situation is shown below:
Fig. 5.4 Tracing an equilibrium path with non-monotonic loading using load control#
For equilibrium paths containing softening behavior, load control might lead to divergence (left) or to large jumps in solution (right) made difficult by a poor initial guess for \(\ba\). Even if equilibrium is found, part of the path becomes effectively inaccessible.
An alternative to overcome this difficulty is to employ Dirichlet constraints and switch to a displacement control approach, the main steps of which are shown below:
Displacement control
Require: Nonlinear relation \(\bff_\mrm{int}(\ba)\) with \(\bK(\ba) = \pder{\bff_\mrm{int}}{\ba}\)
Initialize: \(n=0\), \(\ba^0=\mbf{0}\), partition DOFs into free (\(f\)) and constrained (\(c\))
while \(n<\text{number of time steps}\):
Get new external force vector: \(\bff_\mrm{ext}^{n+1}\)
Initialize new solution at old one: \(\ba^{n+1} = \ba^n\)
Compute internal force and stiffness: \(\bff_\mrm{int}^{n+1}(\ba^{n+1})\), \(\bK^{n+1}(\ba^{n+1})\)
Constrain \(\bK^{n+1}\) so that \(\Delta\ba_c=\bar{\ba}^{n+1}-\bar{\ba}^{n}\)
Evaluate residual at free DOFs: \(\mbf{r} = - \bff_{\mrm{int},f}^{n+1}\)
while \(|\mbf{r}| > \text{tolerance}\):
Solve linear system of equations: \(\bK^{n+1} \Delta\ba = \mbf{r}\)
Update solution: \(\ba^{n+1} = \ba^{n+1} + \Delta\ba\)
Compute internal force and stiffness: \(\bff_\mrm{int}^{n+1}(\ba^{n+1})\), \(\bK^{n+1}(\ba^{n+1})\)
Evaluate residual at free DOFs: \(\mbf{r} = - \bff_{\mrm{int},f}^{n+1}\)
Constrain \(\bK^{n+1}\) so that \(\Delta\ba_c=0\)
Go to the next time step: \(n=n+1\)
Return: Set of internal forces and displacements (equilibrium path)
Note above that \(\bff_\mrm{ext}=\mbf{0}\) at the free nodes, and the residual therefore only contains \(\bff_\mrm{int}\). Naturally, external loads are indirectly applied at constrained nodes in order to move them. Since the equations linked to those DOFs are effectively eliminated from the system, these incurred forces do not appear in the solution scheme but can nevertheless be found during postprocessing by looking at \(\bff_{\mrm{int},c}\) (which, due to equilibrium, cannot be zero). Finally, note that since we are solving for \(\Delta\ba\) and not \(\ba\), \(\Delta\ba_c\) must be constrained to zero after the first iteration of each step: \(\ba\) must already be at the prescribed value after the first linearized solve.
