2.6. Numerical integration

In the discrete equations of the finite element method, integrals appear. These need to be evualated

For example in the 1D Poisson equation it is possible to perform this analytically, as follows.

\[ \mathbf{K}_e = \int_{x_1}^{x_2} \mathbf{B}^T EA \mathbf{B} \,dx \]

\[\mathbf{B} = \left[\begin{matrix}\ B1 & B2\end{matrix}\right]\]

\[ Β1= \frac{1}{x_2-x_1}, Β2= \frac{-1}{x_2-x_1} \]

\[\begin{split} \mathbf{K}_e = \frac{v}{x_2-x_1}\left[\begin{matrix}1 & -1 \\ -1 & 1\end{matrix}\right] \end{split}\]

In practice, however, numerical integration is performed. The idea behind numerical integration is that an integral can be replaced by a weighted sum, as follows:

\[ \mathbf{K}_e = \int_{Ω^ε}\ f(x,y)dΩ \approx \sum_{i=1}^{n_{ip}} w_i f(x_i,y_i) \]

The function \(f\) can be evaluated at a selected number of points, with coordinates \((x_i, y_i)\) and multiplied by weights \(w_i\). The next step involves considering how to perform efficient and accurate numerical integration. One first requirement that arises is that the sum of all weights within an element should be equal to the integration domain, in this case the length of the element. Secondly, the number and location of the integration points must be specified, as well as the individual weights.

The following two integration schemes are relevant for Finite Element Analysis:

• Newton-Cotes

• Gauss Integration

A Newton-Cotes scheme uses equally spaced integration points. In this scheme, with the appropriate set of weights, \(n+1\) integration points are needed to integrate a \(n\)-th order polynomial exactly. Gauss integration (or Gauss quadrature) is more common in finite element analysis. This defines integration locations and weights such that they are optimal in the sense that polynomial functions can be integrated exactly with a minumum number of integration points.

Let’s consider a reference element defined from -1 to +1 in a local \(\xi\)-coordinate. In the Gauss integration scheme the position and weights are optimised for exactly integrating polynomials to as high order as possible.Let’s now look at an example.

• For a O-th order polynomial (\( f= c \)) the position of the integration point is not important, as long as the weight is equal to the length of the domain, which in this case is 2.

• For a 1-st order polynomial (\(f= b ξ + c\)), still we can be exact with one integration point if and only is the integration point is positioned at the centre of ξ-axis.

• For a 2-nd order polynomial (\(f= aξ^2 + b ξ + c\)), exact integration is possible with two integration points, located at \(\xi=\pm 1/\sqrt{3}\) and weight 1. In fact, this integration scheme is also exact for 3-rd order polynomials.

The following rule applies, regarding the order of the polynomial \(p\) that can be integrated exactly for a given number of integration points \( n_{ip} \).

\[ p= 2 n_{ip} -1 \]

This information can be summarised in the following manner.

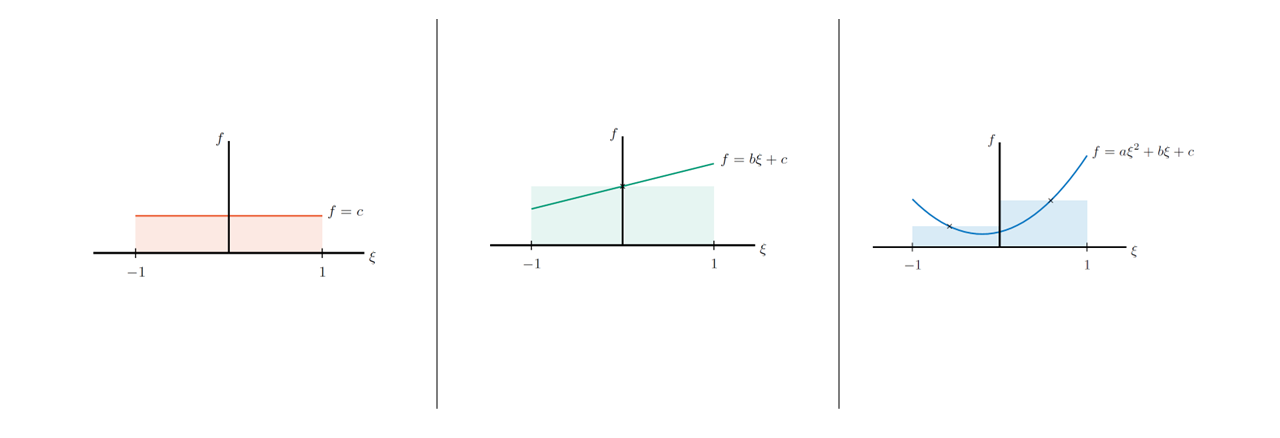
Fig. 2.12 Gauss Integration points

Number of points \(n_{ip} \)	Position \(ξ_i\)	weight	Polynomial order \(p\)
\(1\)	\(0\)	\(2\)	\(0\) or \(1\)
\(2\)	\(-\frac{1}{\sqrt{3}} , \frac{1}{\sqrt{3}} \)	\(1, 1\)	\(2\) or \(3\)
\(3\)	\(-\frac{3}{\sqrt{5}}, 0, \frac{3}{\sqrt{5}}\)	\(\frac{5}{9}, \frac{8}{9}, \frac{5}{9}\)	\(4\) or \(5\)