PyJive workshop: buckling

PyJive workshop: buckling#

This workshop is about analysis of buckling problems with pyjive. Two different modules are applied, the LinBuckModule for linear buckling analysis and the NonlinModule for incrementally-iterative geometrically nonlinear analysis. The main model that is used is the FrameModel.

import matplotlib.pyplot as plt
import numpy as np

import os
import sys

pyjivepath = '../../../pyjive/'
sys.path.append(pyjivepath)

if not os.path.isfile(pyjivepath + 'utils/proputils.py'):
    print('\n\n**pyjive cannot be found, adapt "pyjivepath" above or move notebook to appropriate folder**\n\n')
    raise Exception('pyjive not found')

from utils import proputils as pu
import main
from names import GlobNames as gn

%matplotlib widget

**pyjive cannot be found, adapt "pyjivepath" above or move notebook to appropriate folder**

---------------------------------------------------------------------------
Exception                                 Traceback (most recent call last)
Cell In[1], line 12
     10 if not os.path.isfile(pyjivepath + 'utils/proputils.py'):
     11     print('\n\n**pyjive cannot be found, adapt "pyjivepath" above or move notebook to appropriate folder**\n\n')
---> 12     raise Exception('pyjive not found')
     14 from utils import proputils as pu
     15 import main

Exception: pyjive not found

import contextlib
from urllib.request import urlretrieve

def findfile(fname):
    url = "https://gitlab.tudelft.nl/cm/public/drive/-/raw/main/buckling/" + fname + "?inline=false"
    if not os.path.isfile(fname):
        print(f"Downloading {fname}...")
        urlretrieve(url, fname)

1. Euler Beam#

As a first example, Euler buckling is considered.

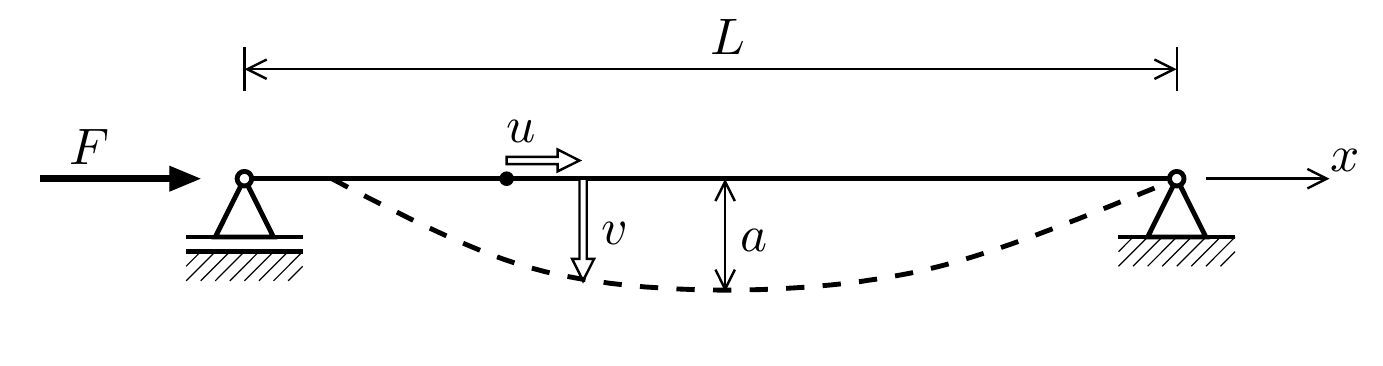
Euler beam
findfile("beam.geom")
findfile("eulerLB.pro")
findfile("eulerNonlin.pro")

Task 1a: Linear buckling analysis

  1. Look in the code to find out how the LinBuckModule and the FrameModel interact. Two scipy linear algebra functions are used, spsolve and eig. What is the function of each of these?

  2. Run linear buckling analysis with the cell below. Print the first 5 buckling values (they are stored in a sorted array in globdat with the key gn.LBFACTORS).

  3. Compare the obtained values to the analytical solution \(F=n^2\pi^2EI/L^2\). What can be done to bring the results closer to the theoretical ones?

props = pu.parse_file('eulerLB.pro')
globdat = main.jive(props)

Task 1b: Geometrically nonlinear analysis

Run the cell below, and inspect the results.

  1. What is the difference between the inputs for the two main.jive calls? How does this affect the model results?

  2. Is the analysis performed in load control or in displacement control?

props = pu.parse_file('eulerNonlin.pro')
globdat = main.jive(props)

props['model']['neum']['values'] = '[ 0.001 ]'

globdat = main.jive(props)

2. Frame buckling#

As a next example, the buckling behavior of a simple frame is analyzed.

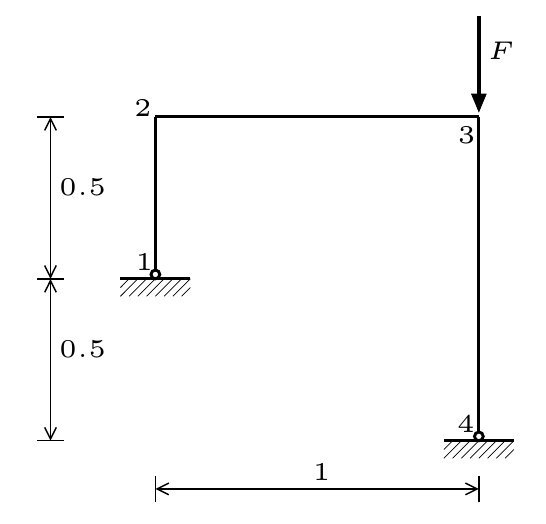
Simple frame
findfile("frame.geom")
findfile("frameLB.pro")
findfile("frameNonlin.pro")

Task 2: Frame buckling

Run the two analyses types by executing the two cells below.

  1. How well do the different analyses agree?

  2. Why does the nonlinear analysis not require an imperfection this time to find buckling behavior?

props = pu.parse_file('frameLB.pro')
globdat = main.jive(props)
print(globdat[gn.LBFACTORS][0:5])

props = pu.parse_file('frameNonlin.pro')
globdat = main.jive(props)

3. Imperfection sensitivity#

The final case concerns analysis of a column that is supported by an inclined elastic spring.

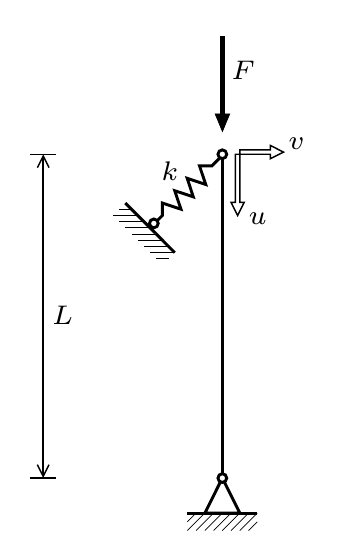
Column supported with inclined spring

An input file is provided where the spring is modeled with a separate FrameModel, with \(EI=GA=0\) and a value for \(EA\) that ensures \(k=1\).

findfile("inclined.geom")
findfile("inclined.pro")

Task 3: Imperfection sensitivity

  1. Inspect the input file inclined.pro. Can you figure out how different properties are assigned to different parts of the model?

  2. Check the influence of moving the top node with an imperfection of \(\Delta=L/100\) to the right. How does this affect the maximum load carrying capacity?

  3. What happens if the imperfection is introduced by moving the top node the same distance to the left?

props = pu.parse_file('inclined.pro')
globdat = main.jive(props)
Contents