8.3. Surrogate model#
Performing multiscale simulations using FE\(^2\) can be advantageous for the aforementioned reasons. However, simulating the Representative Elementary Volume (REV) for the microscale model is not free, and since it needs to be evaluated many times for any macroscopic simulation, FE\(^2\) can quickly become computationally infeasible. For each macroscopic timestep, REVs can be simulated in parallel to speed this process up, but sometimes this is still insufficient. Then, surrogate models can reduce the computational cost by substituting the REV with a cheaper approximate model.
Overview#
Let’s consider a case where we use the REV to find the constitutive relation between the stresses \(\mathbf{\sigma}\) and strains \(\mathbf{\varepsilon}\):
The tangent matrix \(D\) is optionally returned to enable faster macroscopic convergence. Our surrogate method \(\mathcal{S}\) aims to approximate the REV as
The main question is then how we can create \(\mathcal{S}\) such that \(\hat{\mathbf{\sigma}}\) is a good approximation of \(\mathbf{\sigma}\).
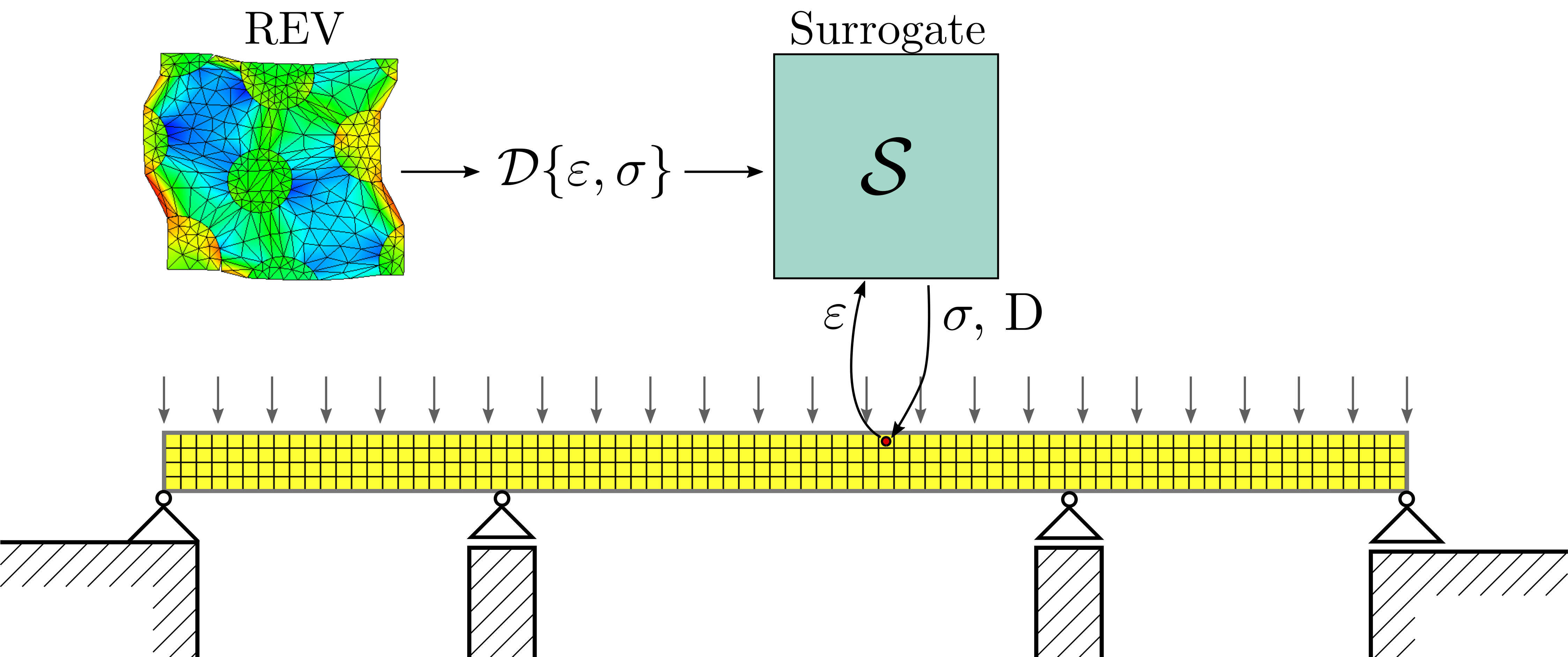
Fig. 8.9 Overview of a multiscale simulation using a surrogate.#
Surrogate design#
Generally, surrogate models are defined by a set of parameters. There are many possible types of surrogate models, such as Proper Orthogonal Decomposition, Gaussian Processes, and various types of neural networks. Especially neural networks are popular, and many variations are actively researched. For a recap on neural networks, we refer to the introduction to Neural Networks in the MUDE online book.
To find the parameters that lead to a good surrogate, we train it on a dataset \(\mathcal{D}\). \(\mathcal{D}\) is created from REV simulation before the full macroscopic problem is simulated. This data generation phase needs to cover a wide range of loading scenarios, as it is not always known which will occur during the actual multiscale simulation. Still, these REV simulations are computationally expensive, so we want to require as few of them as possible.
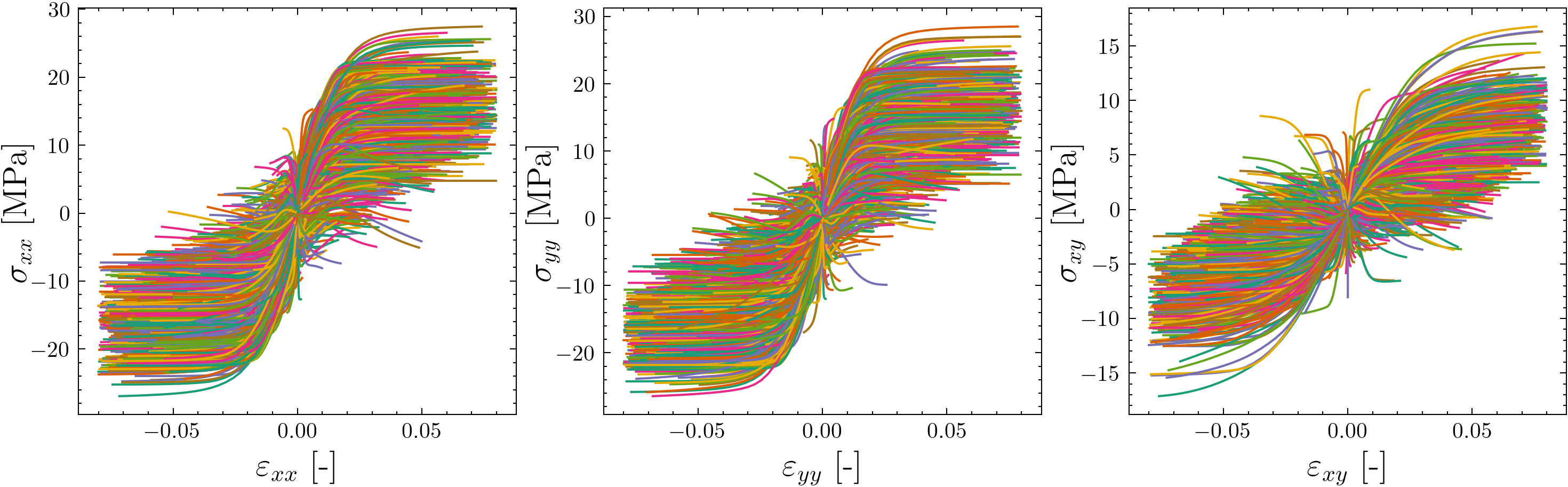
Fig. 8.10 Example of a dataset consisting of 4000 stress-strain curves used to train a surrogate model.#
We train our surrogate \(\mathcal{S}\) by adjusting our parameters \(\mathbf{w}\) to approximate the cases in the training dataset. A common approach is to define a loss function that measures the error of the surrogate. Here we choose a Mean-Squared Error function, and can then define our training process as an optimization problem as
where N is the number of samples in the training dataset \(\mathcal{D}\). In the case of neural networks, the parameters \(\mathbf{w}\) are then iteratively updated using stochastic gradient descent. In practice, minimizing this error will lead to good predictions on all training samples, but poor performance during the simulation due to the model overfitting. This should be avoided by measuring the model using a subset of the dataset (validation set) that is not used to update \(\mathbf{w}\) during the training phase.
The type of surrogate model should be chosen based on the problem requirements. For example, if the REV is history-dependent (e.g. when considering plasticity), then \(\mathcal{S}\) should be able to handle this history dependency too.
Multiscale simulations#
Once the surrogate model has been adequately trained on the generated training data, its parameters stay fixed and the surrogate can be used in the multiscale simulation. The surrogate should be computationally much cheaper than running the REV, allowing the multiscale simulation to be performed in a fraction of the time it would take for a full \(FE^2\) simulation. A trained surrogate can be used for many simulations, as long as its training data is an accurate representation of the simulation of interest. If all training data is generated for specific material properties, then the surrogate can’t be used when these properties change. In such a case a new data generation and training process is required.
Example#
We conclude by showing a recent example of a multiscale simulation whose computational cost has been significantly decreased by using a surrogate model as seen in the figure below. This surrogate has a custom architecture that brings the physical constitutive models from the lower scale inside the neural network. By combining physics and data-driven models, accurate models can be designed that require less training data and perform better outside their training range than their purely data-driven counterparts.
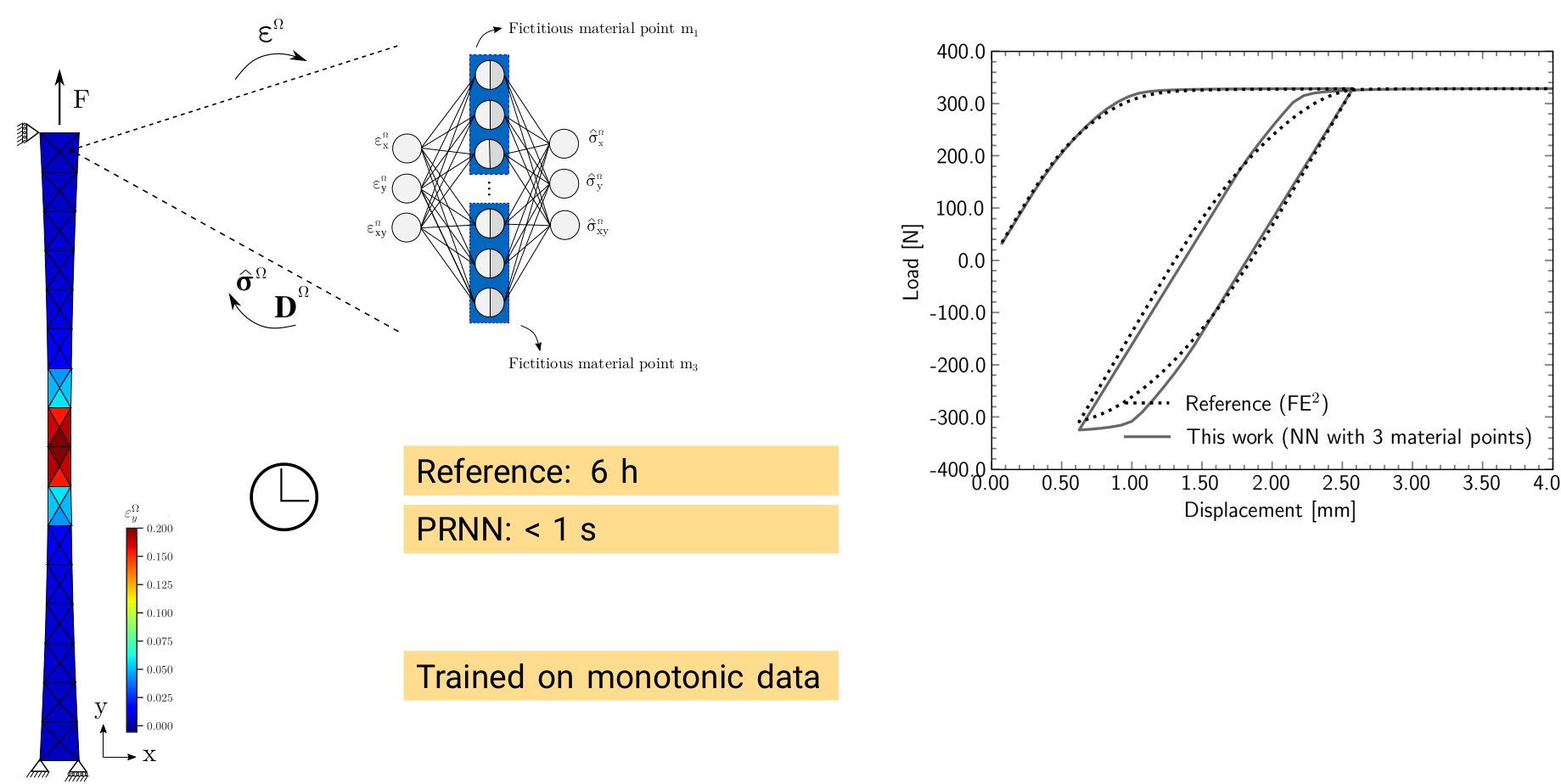
Fig. 8.11 A physically-recurrent neural network is used to drastically accelerate multiscale simulations, while maintaining a high accuracy. From Maia, M. A., et al. “Physically recurrent neural networks for path-dependent heterogeneous materials: Embedding constitutive models in a data-driven surrogate.” Computer Methods in Applied Mechanics and Engineering 407 (2023): 115934.#
