8.1. Urban hydrological processes

So far in this textbook, we have looked at the hydrological processes that occur in a natural environment. The urban environment, on the other hand, is significantly different from a hydrological point of view, with processes occurring at different spatial and temporal resolutions. This results in a change in which the process is dominant, leading to what we call Urban Hydrology (NL: Stedelijke hydrologie). This is largely due to the fact that traditional urban areas are characterized by high levels of surface sealing: rainfall cannot infiltrate the subsurface due to the imperviousness of roads, roofs, and other human interventions. The level of imperviousness also ensures that the water flows more rapidly through the urban environment, facilitated by the presence of underground drainage networks.

Another key difference between urban hydrology and rural hydrology is the presence of underground infrastructure: UDS (Urban Drainage Systems). The boundaries of an urban catchment are dictated by the underlying UDS, where we consider the urban system boundaries to be around the catchment that drains through a UDS. In this textbook, we will consider the most widely implemented form of UDS: the combined sewer system. A combined sewer system discharges wastewater and rainfall through the same conduit, to be discharged either into a WWTP (Wastewater Treatment Plant) or through a CSO (Combined Sewer Overflow). A CSO is a structure that discharges mixed wastewater and rainwater directly into the surface water when the capacity of that system and the WWTP is reached. This is done to prevent wastewater from being discharged onto the street.

In this section, we will look at the urban hydrological processes and highlight how they are different from the natural water cycle.

Note

CSOs will only be considered in their role in the urban hydrological cycle. For more details on their hydrodynamic functioning and impact on water quality, TU Delft BSc Civil Engineering courses Schone Watersystemen and Stedelijk Water en Milieutechniek will have more information.

8.1.1. Urban water cycle

Most of the urban water balance is similar to the natural water balance, the overview of which is given in Section 2.2. The key differences are in the explicit discretisation of pervious (NL: doorlatend) and impervious (NL: verhard) areas, and in the inclusion of drainage networks and drinking water networks. The urban water cycle as a whole can again be understood as a water balance based on the principle of conservation of mass, again typically using volumes instead of masses. The water balance at each of the different storage processes is again:

(8.1)\[ \frac{dS}{dt} = Q_{in} - Q_{out} \quad \text{[L$^3$/T]} \]

with:

\(S\)	Storage	[\(\mathrm{L^{3}}\)]
\(Q_{in}\)	Incoming Fluxes	[\(\mathrm{L^{3}/T}\)]
\(Q_{out}\)	Outgoing Fluxes	[\(\mathrm{L^{3}/T}\)]

Fig. Fig. 8.1 shows all the storage elements and the fluxes between these elements for the urban water cycle. Compare these with Fig. 2.4 to highlight the difference in the processes. Mainly, the inclusion of the drinking and drainage urban water infrastructures are key. In the design process of these systems (which we won’t go into in this course, within TU Delft the course Stedelijk Water en Milieutechniek will), certain design standards have been used. This textbook will consider the Dutch design standards, but note that these apply to the Dutch context alone. Within this module, we will, as is common practice in urban hydrology, consider the deep soil and open water systems as boundary conditions (similar to the atmosphere in Fig. 2.4).

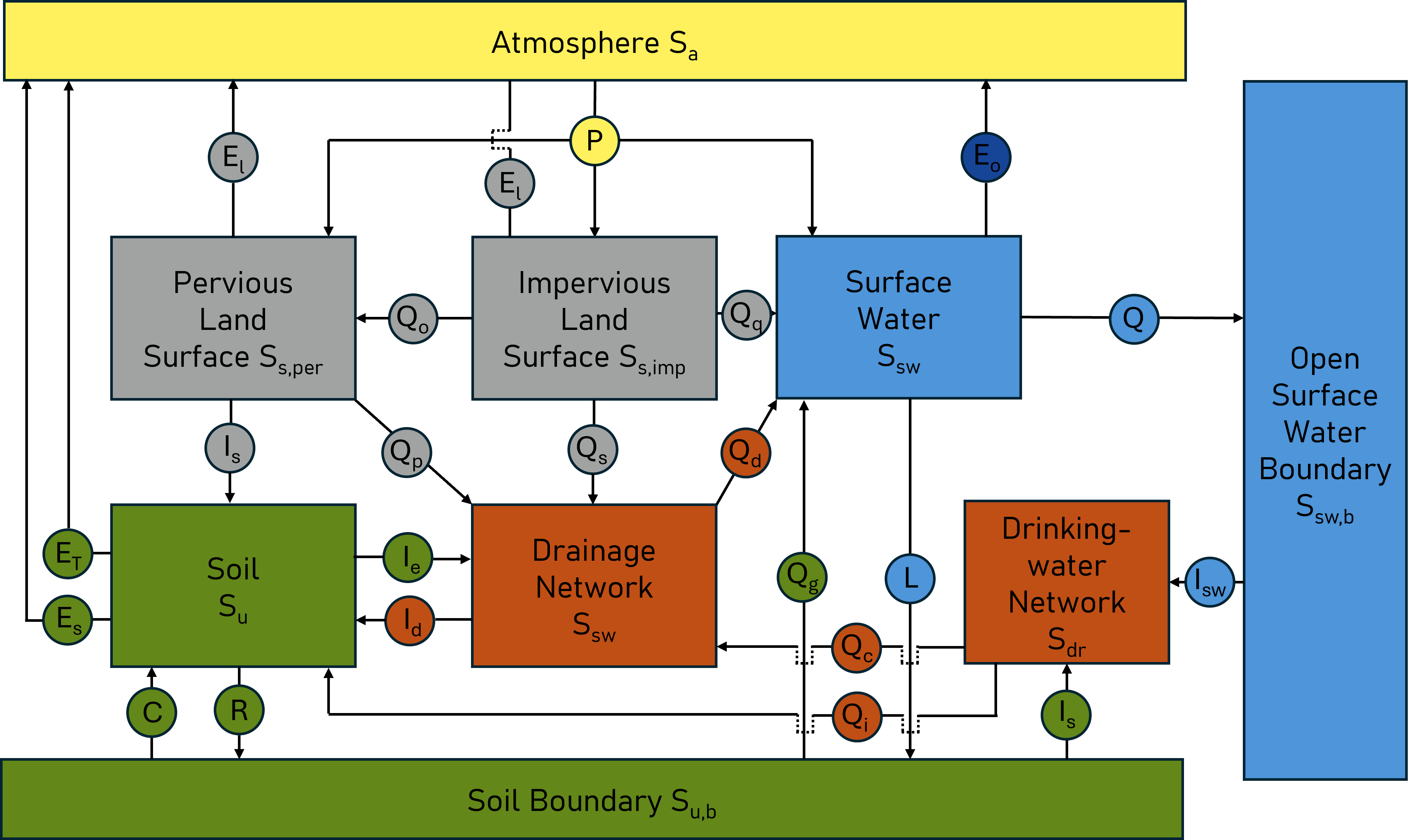
Fig. 8.1 Fluxes and storages of the urban water balance. Fluxes are given as circles, storage components as boxes. (Own work)

8.1.1.1. Urban precipitation

8.1.1.2. Surface storage

The urban surface can be divided into pervious and impervious land cover. As a general rule-of-thumb, impervious land cover is assumed to constitute roughly 70% of an urban area. However, this value varies strongly per location. It can be as high as 90% for city centres and industrial areas or as low as 50% (or even lower) for suburbs.

The urban surface can store water through two different mechanisms: Interception and Depression Storage. Interception consists of the retention of rainfall by the land cover. For pervious land surfaces, this can be quite significant (1-2 mm on vegetation), whereas for impervious land surfaces, the interception is typically neglected (\(<\) 1 mm, stored as the impervious surface “wets”). Depression storage, on the other hand, is the storage in local, small depressions of the surface, i.e., puddles. It occurs on both pervious and impervious land surfaces, and the amount of water that can be stored in depression storage is a function of the surface type and slope expressed in Equation (8.2).

(8.2)\[ d = \frac{k_1}{\sqrt{s}} \quad \text{[L]} \]

with:

\(d\)	Depression storage	[L]
\(k_{1}\)	Surface type coefficient (0.07 for impervious surface and 0.28 for pervious surfaces)	[L]
\(s\)	Surface slope	[-]

Although the two mechanisms can be combined to calculate the total storage, their mechanisms and outward fluxes vary. Specifically, in the pervious land surface, interception storage tends to be depleted through evaporation, whereas depression storage is depleted through infiltration (in the case of pervious land surfaces). For impervious area storage, evaporation is the only significant outward flux.

When the depression and interception storages are filled, urban runoff is generated. This runoff can be routed to another section of the land surface where there is capacity left (e.g., from impervious to pervious land). Alternatively, and most commonly, the water is routed into the underground drainage network through linked gully pots. How water is routed when the storages are filled depends on the design of the city, as it will follow the slope through overland flow.

In recent years, the application of Sustainable Urban Drainage Systems (SUDS) or Blue-Green Infrastructure (BGI) as a way to manage urban water has gained popularity. These methods, which rely on the retention and increased infiltration of stormwater, can be understood as increasing both the pervious area and the depression storage. One of the most common types, the bioswale (NL: Wadi), is a green depression in the landscape where water is routed. Stormwater is captured in these bioswales and allowed to infiltrate within 24 to 48 hours (more information in the section on infiltration).

Fig. 8.2 An example of a bioswale at the TU Delft campus, outside the entrance of the Echo Building. The centre is lower than the pavement around it, allowing the water to run off into the bioswale, effectively increasing the depression storage capacity of the area. As can be seen, water is retained in the bioswale (see the bottom of the picture) and allowed to infiltrate. (Own work)

8.1.1.3. Urban evaporation

8.1.1.4. Drainage network

When the storage capacity of the land surface is exceeded, incoming rainfall becomes urban runoff. This flux, which is a function of the land use and slope, is typically routed to an underground piped network. There are different types of drainage systems, of which the combined sewer system is the most common in the Netherlands (60-70% of the drainage systems are combined). These combined sewer systems convey wastewater and urban runoff through the same conduit. If urban runoff is conveyed, we call this wet weather flow (NL: regenwaterafvoer, RWA). If there is no runoff, we call the sewer flow dry weather flow (NL: droogweerafvoer, DWA). Their inflows are therefore predominantly urban runoff and wastewater. The latter flux (around 120 \(\frac{\text{l}}{\frac{\text{person}}{{\text{day}}}}\)) is the reason why drinking water has to be considered in the urban water balance. A more hidden influx into the sewer network is the infiltration of extraneous water, which occurs when the groundwater level is above the invert level of the sewer system. Although the quantification of this flux is difficult, in some Dutch networks this can be up to 40% of the annual dry weather flow.

The aforementioned influxes can be stored in the conduits of the combined sewer network. As rapid conveyance is difficult due to the flatness of most Dutch cities, combined sewer networks in the Netherlands have a relatively large storage capacity, typically between 6 and 10 mm. There are two key outward fluxes. The first one is the pumping capacity to the WWTP (NL: pompovercapaciteit), usually in the range of 0.5-1 \(\frac{\text{mm}}{\text{hr}}\). The second is a way to avoid combined waste- and urban runoff from ending up on the streets: Combined sewer overflows (CSOs, NL: overstort). These emergency outlets discharge only when the capacity of the sewer network has been reached, and they are an outward flux into surface water systems with a typical design capacity of 20-25 \(\frac{\text{mm}}{\text{hr}}\). Another (less dominant) outward flux is exfiltration, where water infiltrates from the sewer network into the ground. Although this can have strong local implications for local groundwater quality, the total rate from a hydrological perspective is minimal.

The capacity of the sewer network and the pump capacity are parameters that are explicitly designed by urban hydrologists. In order to do this, standard curves can be used. An example of these curves can be seen in Fig. 8.3. Here, curves indicating the annual CSO frequency (i.e., “1” indicates on average a single CSO event can be expected in a year) correspond to a set of pump capacities and sewer storage capacities.

Fig. 8.3 The indicative relation between the storage capacity of a sewer network, its pump over capacity (PoC), and the combined sewer overflow frequency. The curves indicate the overflow frequency for a given combination of PoC and storage capacity. The values are based on 60 years of data using a simplified model. (Own work)

8.1.1.5. Soil

As mentioned previously, the new paradigm in urban hydrology is to encourage the storage of stormwater in the subsurface (soil) as much as possible. Before, because of effective soil sealing with paved areas, almost no water was stored in the soil. The inflow into the subsurface occurs through infiltration. This soil is not permanently saturated, and often before a rainfall event occurs, the soil is unsaturated. The infiltration rate of an unsaturated soil is derived from the same principles used to calculate the flow of groundwater (see Equation (6.10)): water flows from regions with high hydraulic head to regions with low hydraulic head. The key difference is that the hydraulic conductivity of the unsaturated soil is dependent on the soil moisture content (\(\theta\)), which changes as water infiltrates into the soil. This flux of infiltration into the soil is limited by the hydraulic conductivity which can be calculated using Richards’ equation described in the expression below.

(8.3)\[ q_z = -k(\theta) \frac{\partial h}{\partial z} \quad \text{[L/T]} \]

with:

\(q_z\)	vertical flow positive for upward flow	[\(\mathrm{L/T}\)]
\(k(\theta)\)	unsaturated hydraulic conductivity depending on the soil moisture content \(\theta\)	[\(\mathrm{L/T}\)]

The hydraulic conductivity of the unsaturated zone depends on the moisture content of the soil as shown in Equation (8.3). The unsaturated hydraulic conductivity is lower than the saturated hydraulic conductivity because the pores are partly filled with air, limiting the area where flow occurs. The unsaturated hydraulic conductivity increases with increasing soil moisture content. The hydraulic conductivity is highest when the soil moisture content is equal to the porosity of the soil. The flow is thus larger in wet soils compared to dry soils, assuming a constant head gradient.

The relationship between the hydraulic conductivity and the soil moisture content is not linear. The small pores are filled first because the capillary forces are strongest in the smallest pores. As the larger pores are filled, the pores become interconnected and the hydraulic conductivity increases exponentially, as shown in the figure below.

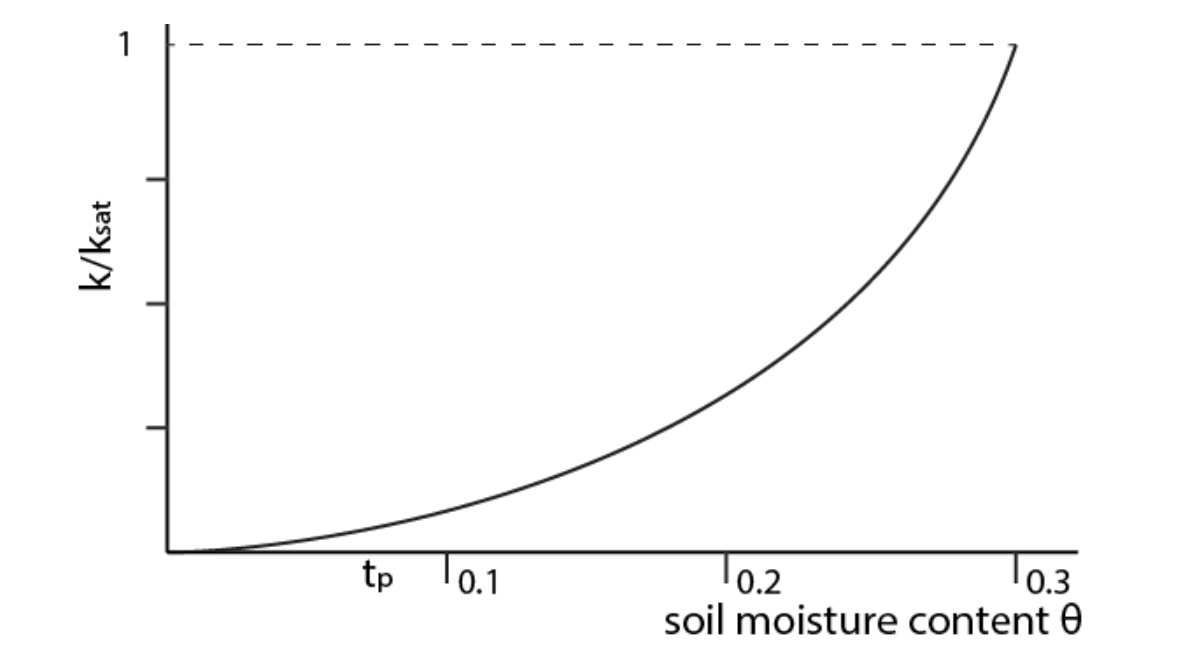
Fig. 8.4 Relationship between the soil moisture content \(\theta\) and the ratio between the hydraulic conductivity \(k\) and the saturated hydraulic conductivity \(k_{sat}\) for a sand soil.

The amount of water that can be stored in the unsaturated subsurface depends on the porosity of the soil itself. For sandy grounds, which are often found in the top layers of a city, this can range between 0.18 - 0.43. Clay soils have a larger porosity (0.4 - 0.7), however, not all pores in the matrix are connected. To better indicate the level of water storage capacity in unsaturated soils, the effective porosity is more commonly used. For clay, this is significantly lower (0.01 - 0.18), whereas the difference between the effective porosity and the total porosity for sand is similar in magnitude.

The outward flux for the unsaturated soil is through evaporation (both soil evaporation and plant transpiration), deep infiltration, and sewer infiltration. Two evaporative fluxes can be identified: soil evaporation and plant and tree transpiration. Both were detailed previously in Section 5.1.1. Deep infiltration is the further infiltration from the unsaturated zone to the saturated zone. Groundwater movement can then move the water outside of the city boundaries. In practical terms, deep groundwater is often neglected as the urban subsurface is complex and heterogeneous, making modeling a difficult task. Infiltration as a process in urban hydrology has, until recently, played a minor role in the overall urban hydrological fluxes. Due to increased damages from urban flooding and damages related to urban heat, BGIs (Blue-Green Infrastructures) were introduced, also known as Sustainable Urban Drainage Systems (SUDS). These forms of infrastructure share the common principle of retaining water in the urban area to allow it to infiltrate. The most common types of BGIs are highlighted in the Table Table 8.1. The infiltration flux for the various BGIs is dependent on the soil composition. As mentioned before, this infiltration capacity is dependent on the saturation rate. This is particularly important if we want to understand the behavior of a BGI during a rainfall event. This behavior is key in understanding the ability of a BGI to reduce runoff: if the infiltration capacity is lower than the rainfall rate, then surface runoff is created.

When we consider a bioswale emptying time, we can assume that the soil underneath the bioswale is fully saturated (the emptying time starts after the rainfall event, during which the soil has become saturated). For this reason, we can use the saturated hydraulic conductivity to estimate the infiltration rate. As the infiltration is vertical in nature (based on the space between the bioswale and the groundwater level), we can assume that the infiltration rate is equal to the hydraulic conductivity of the soil.

Table 8.1 Overview of Blue-Green Infrastructure (BGI) and their processes. (Own work)

BGI	Description	Processes Involved
Green Roof	Green roofs consist of a layer of growing medium (some form of organic sediment) with plants on top. The growing medium can absorb water, which is consequently used for transpiration by the vegetation on top. If the maximum storage capacity of the medium is reached, the water can percolate through the medium to drain away. Green roofs are also excellent insulators and can aid in reducing urban heat effects.	Transpiration, Infiltration, Surface Runoff
Bioswale	A bioswale is a local depression that is vegetated, aiming to retain water during a rainfall event and allowing it to infiltrate over a period of 24-48 hours. Under the swale, the ground has to be sufficiently permeable to allow for this infiltration, and the groundwater level has to be at least 0.5m below it to allow for sufficient infiltration capacity. If these conditions are not met, an underdrain can be installed: a permeable pipe that can aid in the discharge of the infiltrated water. The bioswale has vegetation in it to allow for the evaporation of the water, locally increasing biodiversity and reducing urban heat. If the capacity of a swale is reached, an overflow structure (Dutch: slokop) can be installed to avoid flooding.	Surface Storage, Infiltration, Transpiration
Pervious Pavement	Pervious pavements are non-vegetated pavements that allow water to pass through them, thus reducing surface runoff. Because they do not include vegetation, they can be installed as parking spaces, roads, or other previously designated parts of the urban area. There are limited co-benefits associated with pervious pavements beyond their infiltration capacity.	Infiltration, Surface Runoff
Blue Roof	Blue roofs add storage capacity to retain water on (flat) roofs. The collected water can be released after a rain event, thereby partially attenuating the peak and reducing either CSOs or flooding risks. The water can also be stored and evaporated away, potentially reducing the cooling requirements for a building. Blue roofs can be combined with green roofs in order to store more water and allow the collected water from the blue roof to be used by vegetation.	Storage, Evaporation
Rainwater Harvesting	Rainwater harvesting is the practice of storing rainwater for later use. The most common example of rainwater harvesting practices is the use of a rain barrel in a garden. These rain barrels collect water from the roof and allow the user to use it at a later stage, mainly for irrigation. Harvested rainwater cannot be used for all purposes as the water can potentially be contaminated.	Storage, Water Use

8.1.1.6. Surface Water

The last storage in the urban hydrological cycle is the water stored in surface waters. In the Netherlands, we have both locally controlled urban surface waters (think about canals in a polder) and semi-controlled urban surface waters (for instance, the river Meuse in Maastricht, the water levels of which are only sparingly controlled through human intervention). Those larger rivers are not often considered to be part of the urban hydrological cycle, as their water level depends on the larger catchment.

Smaller, locally controlled urban surface waters (urban canals, e.g. grachten, singels, sloten en kanalen), however, can play a major role in the urban water cycle. Urban canals can typically store approximately 20 mm of runoff. This capacity is maintained through a set of sluice gates and pumps. The urban canals are also related to the groundwater level and can therefore be used to either artificially raise or lower this level. This is of importance in cities as a high groundwater table can lead to flooding or public health issues due to damp basements. Low groundwater tables, on the other hand, which can be achieved by lowering the level in the canals, can have negative consequences on the (wooden) foundation of buildings. Considering the urban hydrological cycle is a key way of maintaining the water level within urban canals. Predictive and reactive control of the water levels can create additional space to avoid urban flooding: if more water can be stored in the canals, less water is likely to end up on the street.

Exercise 8.1

Exercise: Designing a Bioswale

A newly constructed parking lot in Delft is designed to accommodate vehicles while ensuring proper stormwater management. Since impervious surfaces like parking lots generate significant runoff, city planners have decided to integrate a bioswale to capture and store all the runoff from this area.

Your task is to determine the minimum required area of the bioswale to effectively store the runoff generated by the parking lot.

Given Parameters

• Total parking lot area \(A_{parking}\): 60,000 m²

• Existing depression storage on the parking lot \(d_{parking}\): 1 mm

• Target depression storage capacity (with bioswale included) \(d_{target}\): 3 mm

• Surface type coefficient for bioswale \(k_{bioswale}\) is standard

• Surface slope in the bioswale \(s_{\text{bioswale}}\): 0.01

Task

Compute the minimum required bioswale area to obtain the targetted depression storage capacity for the parking lot.

Note: You can manipulate the code cell below by clicking on the “Live Code” (rocket) button in the upper right corner of the book. The first code cell below is for you to practice with. The second one provides the answer to this exercise.

Show code cell content Hide code cell content

# --------------------------------------- DO NOT MODIFY THIS ----------------------------------- #

# Given parameters - DO NOT MODIFY THIS
A_neighborhood = 60000  # Total neighborhood area in m²
storage_current = 1 / 1000  # Current depression storage in meters (3 mm)
storage_target = 5 / 1000  # Target depression storage in meters (5 mm)
storage_increase = storage_target - storage_current  # Increase in storage required
V_needed = A_neighborhood * storage_increase  # Volume of water to be stored by the bioswale
s_bioswale = 0.01  # Surface slope for bioswale

# --------------------------------------- MODIFY THIS ------------------------------------------ #

# Bioswale parameters - MODIFY THIS
k_bioswale = 0 ## FILL IN YOUR VALUE HERE

# Compute the depression storage capacity of the bioswale - MODIFY THIS
d_bioswale = 0 ## FILL IN A FORMULA HERE

# Compute the required bioswale area - MODIFY THIS
A_bioswale = 0 ## FILL IN A FORMULA HERE

# --------------------------------------- DO NOT MODIFY THIS ----------------------------------- #

# Display result
print(f"Required bioswale area: {A_bioswale:.2f} m²")

# Check student answer - DO NOT MODIFY THIS
tolerance = 0.5  # Acceptable deviation
if abs(A_bioswale - 85.71) <= tolerance:
    print("✅ Correct! Your calculated bioswale area is within the expected range.")
else:
    print(f"❌ Incorrect. The correct bioswale area can be found in the code cell below.")

Required bioswale area: 0.00 m²
❌ Incorrect. The correct bioswale area can be found in the code cell below.

Show code cell content Hide code cell content

# --------------------------------------- DO NOT MODIFY THIS ----------------------------------- #

# Given parameters - DO NOT MODIFY THIS
A_neighborhood = 60000  # Total neighborhood area in m²
storage_current = 1 / 1000  # Current depression storage in meters (3 mm)
storage_target = 5 / 1000  # Target depression storage in meters (5 mm)
storage_increase = storage_target - storage_current  # Increase in storage required
V_needed = A_neighborhood * storage_increase  # Volume of water to be stored by the bioswale
s_bioswale = 0.01  # Surface slope for bioswale

# --------------------------------------- MODIFY THIS ------------------------------------------ #

# Bioswale parameters - MODIFY THIS
k_bioswale = 0.28 ## TYPICAL SURFACE TYPE COEFFICIENT FOR BIOSWALE

# Compute the depression storage capacity of the bioswale - MODIFY THIS
d_bioswale = k_bioswale / (s_bioswale ** 0.5) ## FORMULA FOR DEPRESSION STORAGE CAPACITY

# Compute the required bioswale area - MODIFY THIS
A_bioswale = V_needed / d_bioswale ## COMPUTE THE AREA USING THE VOLUME AND THE DEPRESSION STORAGE CAPACITY

# --------------------------------------- DO NOT MODIFY THIS ----------------------------------- #

# Display result
print(f"Required bioswale area: {A_bioswale:.2f} m²")

Required bioswale area: 85.71 m²