The process of evaporation

5.1. The process of evaporation#

Evaporation (NL: verdamping) is the transfer of water from a liquid state into a gaseous state. Within the framework of hydrological processes, it usually means the average vertical vapor transport over an area. To evaporate water, the atmosphere should be able to hold the water vapor and there should be a transport mechanism. The latter is provided by turbulence, where eddies can transport the water vapor upwards. Turbulence can be caused by wind blowing over a rough surface (i.e., mechanical turbulence) or by radiation (i.e., buoyancy). In hydrological applications, evaporation is mostly expressed in water depth per time (e.g., mm/d), but as evaporation of water requires energy we can also express evaporation in terms of energy. Often then the term latent heat flux (NL: latente warmtestroom) is used and the unit is then e.g., W/m$^2$ or J/m$^2$/d (note: 1 W = 1 J/s). Evaporation and latent heat can easily be converted into each other by multiplying the evaporation (m/s) with the density of water ($\rho=1000$ kg/m$^3$) and the latent heat of vaporization ($\lambda_w$). The latent heat of vaporization for a set temperature is defined as the amount of energy (Joule) used at that temperature to transfer 1 gram of water from liquid state into water vapor. The dependence of $\lambda$ on temperature is proven to be minor. That is why $\lambda$ is taken as a constant in practice: $\lambda = 2.45⋅10^6$ J/kg.

The beauty that the transport of water to the atmosphere can be expressed in terms of water (e.g., mm/day) or in terms of energy (e.g., W/m$^2$), enables that studying evaporation can be done by using the water balance and by using the energy balance:

(5.1)#\[\begin{split} \frac{\textrm{d}S}{\textrm{d}t}=P-E-Q \\ \end{split}\]

(5.2)#\[ \frac{\textrm{d}S_Q}{\textrm{d}t}=R_n-\rho \lambda E-H-G \]

Similar to the water balance (see Chapter 2.2), a balance can be made where the net radiation (NL: netto straling, $R_n$) can be used to:

evaporate water (latent heat flux, NL: latente warmtestroom, $\rho \lambda E$);
heat the atmosphere (sensible heat flux, NL: convectief warmteflux , $H$);
warm up the ground (ground heat flux, NL:bodem warmteflux, $G$).

The difference is the heating of the globe ($\frac{\textrm{d}S_Q}{\textrm{d}t}$), which can often be neglected at hydrological time scales(time scales shorter than one century).

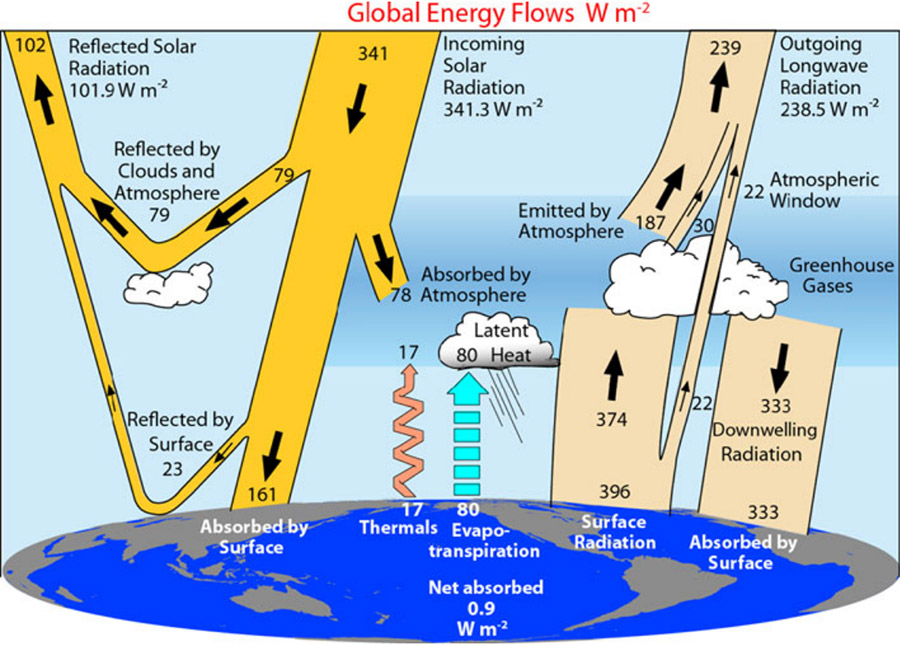
../_images/5_1_1-global_energy_flow.png — Fig. 5.2 Global energy flow (Kevin Trenberth, John Fasullo and Jeff Kiehl, n.d.)#

# Note that the code cell below is used for the website only

Exercise 5.1 (Energy balance)

Consider a day with a net radiation of 100 W/m$^2$. The sensible heat flux is 20 W/m$^2$ and the ground heat flux is assumed to be 10% of the net radiation. There is ample water available in the unsaturated zone.

a) What would be the latent heat in this situation in W/m$^2$?

b) And the evaporation in mm/d?

c) After a long dry spell the unsaturated zone is completely dried out. How will this alter the energy fluxes?

5.1.1. Types of evaporation#

Evaporation can occur from any water surface, the soil, or via vegetation. A water surface can be open water (e.g., a lake, pool, pond), or any (temporarily) wet surface (e.g., a wet canopy, a wet roof). Evaporation from a wet surface is also called interception evaporation, as a part of the rainfall is intercepted and temporarily stored on the wetted surface from where it can evaporate. Open water evaporation (NL: open waterverdamping), interception evaporation (NL: interceptieverdamping) and soil evaporation (NL: bodemverdamping) are also called direct evaporation or non-productive evaporation (NL: niet-productieve verdamping). This is opposite to indirect or productive evaporation, where water is transported via plants. The term productive relates to the fact that biomass is formed as well.

Direct/non-productive evaporation:
- Open water evaporation, $E_o$ [L/T]: This is the amount of vaporized water within a certain time from an open water surface. The availability of the water is hereby not restricted.
- Soil evaporation, $E_s$ [L/T]: The water that is vaporized is soil moisture. When the moisture content is limited, the evaporation is more constrained.
- Interception evaporation, $E_i$ [L/T]: Evaporation from the wet surface after rainfall. It contains evaporation from all wet surfaces: vegetation, paved surfaces, dropped leaves, bare soil, etc. So more than just interception by leaves.
Indirect/non-productive evaporation:
- Transpiration (NL: transpiratie) $E_t$ [L/T]: The transfer of water into the atmosphere through the stomata of living plants. Just a very small amount of the water absorbed by plants from the soil remains inside the plant itself. The major part vaporizes from the leaves. Because of the influence of solar radiation, transpiration occurs primarily during daytime. At night the pores close and little water leaves the plant. An exception is for instance the cactus (the stomata only open at night).

To summarize, direct evaporation is the transfer of liquid into vapor by molecules that escape the water surface; transpiration is a physiological process of water molecules transferring by gas exchange in the stomata from the vegetation into the atmosphere.

The total amount of water vapor transported to the atmosphere is the sum of all occurrences of evaporation:

(5.3)#\[ E_{tot} = E_o + E_s + E_i + E_t \]

Sometimes in literature, this term is wrongly referred to as evapotranspiration (Miralles et al., 2020, Savenije, 2004). If this term is used, it is recommended to carefully check what is meant by evapotranspiration as sometimes the total evaporation is meant, but sometimes evapotranspiration only refers to the transpiration process.

5.1.2. Definitions#

As hydrologists, we would like to know the actual amount of water vapor that is transported to the atmosphere. However, determining this actual amount is very difficult as measuring evaporation is neither easy nor cheap (see later section 5.2) resulting in limited data availability about actual evaporation. Easier to determine is the maximum amount of water that could evaporate if there is no restriction on the water available. This maximum amount is called the potential evaporation (NL: potentiele verdamping, $E_p$) and often only requires meteorological input. Potential evaporation does not consider the water availability and therefore should be seen as an upper boundary of the maximum possible amount of evaporation. If water is abundant, actual and potential evaporation are equal. But as soon as the water availability drops, the actual evaporation ($E_a$) will also drop. Thus per definition: $E_a \leq E_p $ [L/T]. If there is no water $E_a$ will be zero, but the potential evaporation can still be high.

Farmers also often use estimates of potential evaporation to determine how much irrigation water their crops need. However, for this purpose, they also have to consider that the potential evaporation of a crop is not only dependent on meteorological input. Crops have a certain resistance against evaporation (stomata opening and closing costs energy) causing the potential evaporation of a crop to be lower in comparison to the potential evaporation of e.g., a lake. A widely used framework to estimate the potential evaporation of a crop ($E_{p, crop}$) is the framework of the Food and Agriculture Organization (FAO) of the United Nations (Allen et al., 1998). They defined the so-called reference evaporation (NL: referentieverdamping, $E_{ref}$), which is the potential evaporation of a well-watered grass field of 12 cm height:

(5.4)#\[ E_{ref} = E_{p, grass} \quad \text{[L/T]} \]

In literature (e.g., Allen et al. (1998)) tables can be found that describe the relation between this reference crop (i.e., grass) and other crops by means of a crop factor ($k_c$). This crop factor can also consider the growing stage of the plant. The FAO-method assumes that there is a linear relation between the reference evaporation and the potential evaporation of a crop in a certain growing stage:

(5.5)#\[ E_{p, crop} = k_c \times E_{ref} \quad \text{[L/T]} \]

Similarly, the FAO-method also assumes a linear relation between potential and actual evaporation. For this purpose, they defined a stress factor ($k_s$), which accounts for water shortage:

(5.6)#\[ E_{a, crop} = k_s \times E_{p, crop} \quad \text{[L/T]} \]

If water is abundant, $k_s$ equals one. If no water is available, $k_s$ drops to zero. As actual evaporation is per definition lower than the potential evaporation, $k_{s}$ is per definition smaller or equal to one.

Although the FAO-method is from a practical point of view very easy to use, its physical meaning is doubtful as the determination of the crop and stress factors are highly empirical and difficult to determine in practice.

5.1.3. Factors influencing evaporation#

The energy for evaporation is, directly or indirectly, provided by solar radiation. The amount of radiation that is available for evaporation depends on the latitude, the time of the year, atmospheric conditions like the cloudiness, reflection by the Earth’s surface, atmospheric absorption and storage capacity of the ground or the water. To keep the process of evaporation going, the water vapor has to be removed from the evaporating surface (e.g., by wind). This is a process of diffusion and turbulent transport which is affected by the humidity and temperature of the air, the roughness of the surface and the wind speed. For plants, the resistance to flow of water inside the plant and the percentage of the soil covered by crops do influence evaporation rates as well.

Thus the (potential) evaporation is affected by factors which are determined by:

a. Evaporation surface
b. Atmospheric conditions

Hereafter we will elaborate on the important influencing factors.

For a bare evaporation surface or with open water (i.e., direct evaporation), the following factors are important:

a.1. Reflection coefficient (albedo): As solar radiation hits the surface a part of this radiation will be reflected back. The surface properties determine how much radiation is reflected. For example a black surface (e.g., water) will absorb a high amount, while a white surface (e.g., snow) will reflect almost all of the incoming solar radiation. Typical values for the reflection coefficient or albedo ($r$) of solar radiation reaching the earth’s surface are given in table Table 5.1. For the influence of reflection on evaporation see the paragraph about solar radiation.

Table 5.1 Albedo ($r$) for different surfaces (Brutsaert, 2005)#
Surface	Albedo
Open water surface	0.04 - 0.08
Grass	0.15 - 0.25
Bare fields	0.15 - 0.25
Fresh snow	0.80 - 0.90

a.2. Roughness of the surface: The turbulent transport of water vapor from the evaporating surface into the atmosphere is largely determined by the roughness (e.g., crop height) of the surface. The resistance to this transport is called the aerodynamic resistance ($r_a$) and may for a specific surface (roughness) be written as a function of the wind speed (see the paragraph about wind velocity). For a rough surface, the (mechanical) turbulence is higher so water can be transported more easily. This results in a lower aerodynamic resistance value and a higher evaporation rate.
a.3. Heat storage capacity: In climates with a distinct summer and winter period, part of the energy that becomes available in spring is used to warm up the surface. This energy is released during the next autumn and winter. A deep lake or wet soil has a large heat storage capacity. Hence, the evaporating surface will remain relatively cold during spring which affects the evaporation. The subsequent release of heat during the autumn and winter causes a phase shift in the evaporation cycle of deep lakes as compared to shallow lakes. In the case of soil, this heat exchange is called the ground heat flux ($G$).

For a surface with vegetation, two factors are added:

a.4. Fraction covered: The fraction of soil that is covered by the crop directly affects the transpiration of the area.
a.5. Crop resistance: Transpiration of a cropped surface is usually less than the evaporation of an open water surface due to the additional resistance of water transport in the plant and the transfer of water vapor through the stomata. This additional resistance is called crop resistance, $r_c$. For tall crops, however, the increased turbulence lowers the aerodynamic resistance $r_a$ which may result in higher values for the transpiration as compared to open water evaporation. The crop resistance is often taken from literature or can be estimated by e.g., the Jarvis-model (Jarvis, 1976) where solar radiation, temperature, vapor pressure deficit, and leaf water potential determine the crop resistance. This model also accounts for the water availability. As there is no water the $r_{c}$ will become infinite. Although the crop resistance and the crop factor of the FAO-method ($k_c$) are related, they should not be mixed up.

The atmospheric conditions which influence the evaporation:

b.1. Wind velocity: The aerodynamic resistance to water vapor transport $r_a$ [T/L] is a function of the wind speed. Wind speed is measured with anemometers and is a function of the height above the surface. Values that apply for a height of 2 m are generally used to estimate evaporation. The wind speed of other heights can by approximation be conversed to wind speed at 2 m. The aerodynamic resistance to water vapor transport is computed with the formula (Penman, 1956):

(5.7)#\[ r_a = \frac{245}{(0.54u_2+0.5)} \]

with $r_a$ in s/m, and $u_2$ as the wind speed (m/s) measured at a height of two meters.

b.2. Relative humidity (NL: relatieve vochtigheid): Evaporation is very sensitive to the humidity of the air at a constant temperature. If the atmosphere is completely saturated, evaporation is difficult: the atmosphere can not hold more water vapor. The relative humidity expresses the amount of water vapor present in air expressed as a percentage of the amount needed for saturation at the same temperature. Humidity is often expressed in terms of vapor pressure (kPa). Vapor pressure is the pressure of water particles in the atmosphere. If the atmosphere is completely saturated, the pressure equals the saturated vapor pressure (NL: verzadigingsdampspanning), $e_s$. Saturated vapor pressure is a function of temperature $T$: the higher the temperature, the more water can be stored in the atmosphere. The relation between temperature $T$ and $e_s$ is called the Clausius Clapeyron equation (Koutsoyiannis, 2012):

(5.8)#\[ e_s(T) = 0.61 \exp \bigg(\frac{19.9T}{273+T}\bigg) \quad \text{[kPa]} \]

where $T$ is the temperature in °C. In figure Fig. 5.3 the equation is shown as a graph.

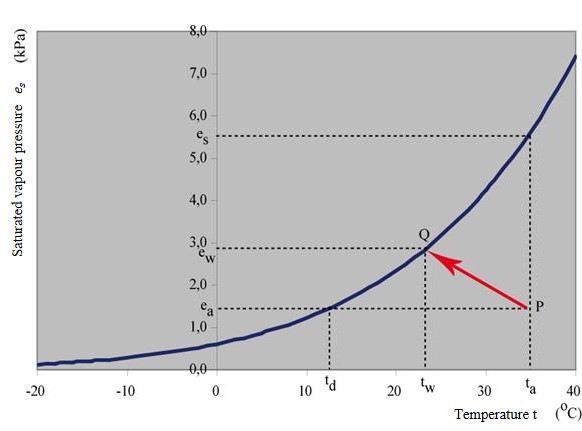
../_images/verzadigingsdampspanning.jpg — Fig. 5.3 Saturated vapor pressure#

However, the atmosphere is not always fully saturated. The actual amount of water vapor, expressed in pressure, is called the actual vapor pressure (NL: daadwerkelijke dampspanning), $e_a$ [kPa]. The ratio of actual and saturated vapor pressure is the relative humidity:

(5.9)#\[ h = \frac{e_a(T)}{e_s(T)} \times 100\% \quad \text{[-]} \]

Thus, the relative humidity determines the ‘available space’ for water vapor in the atmosphere. Sometimes this ‘space’ is also defined as the vapor pressure deficit [kPa]: $e_s(T)-e_a(T)$. There are three ways to determine the actual vapor pressure:

By the relative humidity: In case of direct measurement of the relative humidity (e.g., by a hygrometer) and the air temperature ($T_a$): $e_a(T_a)=h \times e_s(T_a)$
By dew point (NL: dauwpunt): Some meteorological organizations provide the dew temperature $T_d$. Dewpoint temperature is the temperature where saturation occurs given a certain actual vapor pressure. At this point, we know that we are on the saturated vapor pressure line and thus the following relation holds: $e_s(T_d)=e_a(T_a)$. Graphically, this means that you move from a point P in Figure Fig. 5.3 horizontally to the left until you hit the saturated vapor pressure line. The temperature where this happens is called the dew point temperature.
By a psychrometer: A psychrometer consists of two thermometers, a dry one and one in a wet state (often by adding a wet cloth around it). When there is no airflow both thermometers will have the same value ($T_a=T_w$). But when an air flow is forced past the thermometers, this will result in a lower temperature of the wet thermometer ($T_w$) than of the dry ($T_a$) one due to the extraction of energy of latent heat for the evaporation of water from the wet thermometer. The amount of energy that is extracted is determined by the psychrometric constant ($\gamma=0.066$ kPa/°C). The temperature of the wet thermometer is called wet bulb temperature (NL: natteboltemperatuur). In figure Fig. 5.3 the line $PQ$ indicates the situation of a humid medium (e.g., a wet patch) cooling down under the influence of ventilation from the actual temperature $T_a$ to ‘wet’ temperature $T_w$. The evaporation involved in this process causes a drop in temperature until a new equilibrium is reached in point $Q$. At this point, the vapor pressure is increased to the saturated vapor pressure of a wet medium $e_s(T_w)$. Note that $\gamma$ gives the slope of the line $PQ$. Successively, we can compute the actual vapor pressure (NL: daadwerkelijke dampspanning) [kPa] with the formula:

(5.10)#\[ e_a(T_a)=e_s(T_w)-\gamma(T_a-T_w) \quad \text{[kPa]} \]

With:


$e_s(T_w)$	computed with Equation (5.8)	[kPa]
$T_a$	Air temperature	[°C]
$T_w$	Wet bulb temperature	[°C]
$\gamma$	psychrometer constant	[0.066 kPa/°C]

# Note that the code cells below is used for the website only.

Exercise 5.2 (Psychrometer/humidity)

a) What is the relative humidity for an air temperature of 18 degrees Celcius and a wet bulb temperature of 10 degrees?

b) If the humidity is 100% what will be the wet bulb temperature?

For some computations the slope of the saturation vapor pressure curve ($s$ = $\textrm{d}e_a$/$\textrm{d}T$) is important. This is easily determined by the derivative of Equation (5.8):

(5.11)#\[ s(T) = \frac{\textrm{d}e_s}{\textrm{d}T} = \frac{5430e_s}{(273+T)^2} \quad \text{[kPa/C°]} \]

b.3. Solar radiation: Evaporation is direct or indirect, provided by solar energy. Solar radiation is therefore the most dominant factor for the determination of evaporation. The radiation coming from the sun (i.e., hot body) is called shortwave radiation (NL: kortegolfstraling, wavelengths 0.3 - 3 μm). The radiation that is received at the outer limits of the atmosphere is called extraterrestrial radiation ($R_a$) and is dependent on the latitude and the time of the year. Due to local atmospheric conditions (e.g., smog) and cloudiness the amount of shortwave radiation entering the Earth’s surface is reduced. This reduced radiation is called incoming shortwave radiation ($R_{s,in}$) and is important for the evaporation process. Often the incoming shortwave radiation is directly measured at the earth’s surface by pyrometer, but can also be estimated by empirical relations between $R_a$ and the cloudiness ($n$/$N$). Where $n$ is the number of actual hours of sunshine and $N$ is the number of possible hours of sunshine (depending on the time of year and location). In general, the relation between extraterrestrial and shortwave radiation can be expressed as (Hendriks, 2010):

(5.12)#\[ R_{s,in} = (a_s + b_s \frac{n}{N}) * R_a \]

For the Netherlands, typical values for the constants are $a_s=0.2$ and $b_s=0.55$ (De Bruin and Stricker, 2000), while globally often $a_s=0.25$ and $b_s=0.5$ (Allen et al., 1998) are recommended. Other estimates can be found in (Iqbal, 1983). As mentioned before, a part of the incoming shortwave radiation is immediately reflected back. Hence the net shortwave radiation equals $R_{s,in}-R_{s,out}=R_{s,in} - rR_{s,in}=(1-r)R_{s,in}$, where $r$ is the albedo.

Similar to a hot body (sun) that emits shortwave radiation, a cold body with temperature $T$ emits longwave radiation (NL: langegolfstraling, wavelengths 5 - 100 μm). Both the earth and the atmosphere are such cold bodies. Longwave radiation follows the law of Stefan Bolzmann: $R_{l, out}=\epsilon \sigma (T+273)^4$. Where $\epsilon$ is the emissivity coefficient, $\sigma$ the Stefan Bolzmann coeficient ($=5.67 \times 10^{-8}$ W $m^{-2}$ $C^{-4}$ $= 4.9 \times 10^{-3}$ $J$ $d^{-1}$ $m^{-2}$ $C^{-4}$), and $T$ the temperature of the surface ($T_s$) or atmosphere ($T_a$) in Celsius. The surface emits longwave radiation back to the atmosphere ($R_{l, out}$) and is dominant in comparison to the atmosphere that emits longwave radiation towards the earth ($R_{l, in}$). As the determination of the emissivity is complex, often an emprical relation is used where the net outgoing longwave radiation ($R_{l, out}-R_{l,in}$) equals:

(5.13)#\[ R_{l,n}=R_{l, out}-R_{l,in}=\sigma (T+273)^4 (a_e+b_e \sqrt(e_a))(a_c+b_c\frac{n}{N}) \]

Typical values for the constants are: $a_e=0.34$, $b_e=-0.14 kPa^{0.5}$, $a_c=0.25$, and $b_c=1-a_c=0.75$ (Hendriks, 2010). For estimating evaporation the net radiation, $R_n$ is important. It is the balance between all incoming and outgoing radiation fluxes (see Figure Fig. 5.4):

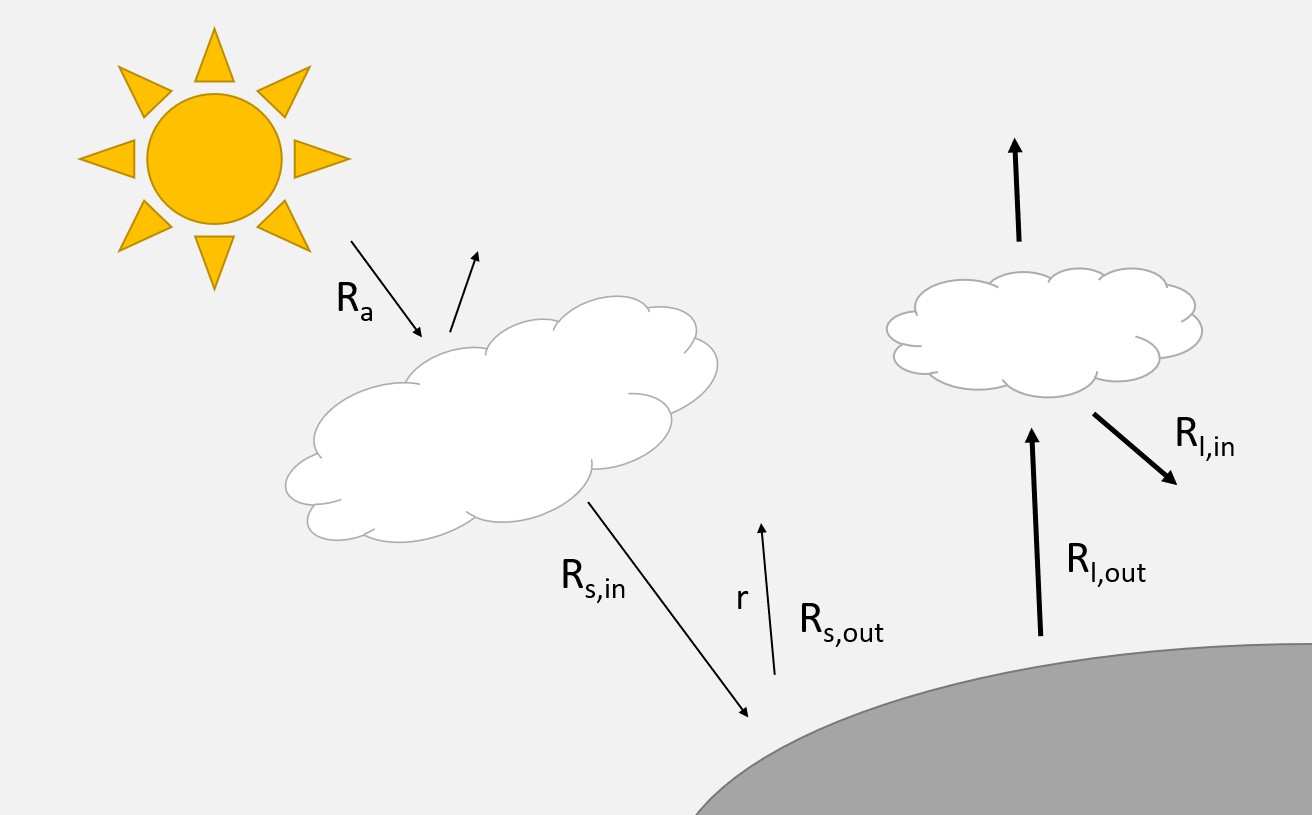
../_images/RaRbenRc.JPG — Fig. 5.4 Incoming and outgoing radiation (R).#

(5.14)#\[ R_n = R_{s,in} - R_{s,out} + R_{l,in} - R_{l,out} = R_{s,in} - rR_{s,in} - R_{l,n} =(1-r)R_{s,in}-R_{l,n} \quad \text{[Jd$^{-1}$m$^{-2}$]} \]

The net radiation can be measured with a radiometer (see Fig. 5.5).

../_images/radiometer.jpg — Fig. 5.5 Radiometer#

b.4. Temperature: The saturated vapor pressure of the air is a function of the temperature of the air ($T_a$). The longwave radiation is temperature-dependent as well. To measure the temperature properly, only air temperature has to be measured, hence the energy should be supplied by convection and not by radiation, condensation or conduction. For that, the thermometer needs to be naturally ventilated and sheltered from sun and rain. This can be done according to the WMO standard in a ‘Stevenson shelter’ (Fig. 5.6).

../_images/Stevensonshelter.jpg — Fig. 5.6 Stevenson Shelter#


\(e_s(T_w)\)	computed with Equation (5.8)	[kPa]
\(T_a\)	Air temperature	[°C]
\(T_w\)	Wet bulb temperature	[°C]
\(\gamma\)	psychrometer constant	[0.066 kPa/°C]

The process of evaporation

Contents

5.1. The process of evaporation#

5.1.1. Types of evaporation#

5.1.2. Definitions#

5.1.3. Factors influencing evaporation#