6.4. Additional exercises

Exercise 6.8

An aquifer is bounded by two long, deep rivers. The distance between the rivers is \(L\). Groundwater recharge is uniform everywhere and equal to \(N\). The water level in the river is \(h_l\) on the left and \(h_r\) on the right. The aquifer’s permeability is \(k\). The saturated thickness \(D\) of the aquifer can be approximated as constant. Groundwater flow in the aquifer is steady-state and one-dimensional. A vertical cross-section of the aquifer is shown in the figure, with the origin of the x-axis chosen as indicated.

Fig. 6.25 Aquifer bounded by rivers.

The following is known:

\(k\) = 13 m/d, \(D\) = 10 m, \(h_l\) = 8.9 m, \(h_r\) = 8 m, \(L\) = 800 m.

Known is that at \(x\) = \(L/3\) m, the groundwater level is \(h\) = 9.4 m. What should be the groundwater recharge in mm/d?

Answer Exercise 6.8

The given equation is:

\[ h(x) = \left(-\frac{N}{2KD}\right)x^2 + Ax + B \]

Boundary conditions:

\[ x = 0 \qquad \rightarrow \qquad h = h_l \]

\[ x = L \qquad \rightarrow \qquad h = h_r \]

Calculate \( B \) when \( x = 0 \):

\[ h(x=0) = \left(-\frac{N}{2KD}\right)0^2 + A\cdot0 + B = B \]

\[ h(x=0) = h_l = 8.9 \text{ m} \]

Now, substitute \( B = 8.9 \) into the equation. At \( x = L \):

\[ h(x=L) = \left(-\frac{N}{2KD}\right)L^2 + AL + 8.9 \]

\[ h(x=L) = h_r = 8 \text{ m} \]

Solving for \( A \):

\[ -0.9 \text{ m} = \left(-\frac{N}{2KD}\right)L^2 + AL \]

\[ A = -\frac{0.9}{L} + \frac{NL}{2KD} \]

Substitute \( A \) and \( B \) back into the original equation:

\[ h(x) = \left(-\frac{N}{2KD}\right)x^2 + Ax + B \]

\[ h(x) = \left(-\frac{N}{2KD}\right)x^2 + x\left(-\frac{0.9}{L} + \frac{NL}{2KD}\right) + 8.9 \]

Given that at \( x = \frac{L}{3} \), the groundwater level is 9.4 (with \( L = 800 \)):

\[ h\left(\frac{800}{3}\right) = \left(-\frac{N}{2 \times 13 \times 10}\right)\left(\frac{800}{3}\right)^2 + \frac{800}{3}\left(-\frac{0.9}{800} + \frac{N \times 800}{2 \times 13 \times 10}\right) + 8.9 = 9.4 \]

Solving for \( N \):

\[ 0.8 = 820N - 273.5N \]

\[ 547N = 0.8 \]

\[ N = 0.00146252 \text{ m/d} = 1.463 \text{ mm/d} \]

So, the groundwater recharge is approximately 1.463 mm/d.

Exercise 6.9

A phreatic aquifer is separated from a deeper aquifer by a horizontal clay layer. In the lower aquifer, water is pumped, causing the specific discharge downward through the clay layer to be 2 mm/d. The phreatic specific yield of the upper aquifer is 0.1.

How much does the groundwater level in the upper aquifer drop in 1 week if there is no groundwater recharge?

Answer Exercise 6.9

Using the water balance:

\[ \text{In - Out - Change in storage} = N dt - q_z dt - S dh = 0 \]

As \(N=0\):

\[ dh = \frac{-q_z dt }{S} = \frac{2 \cdot 7}{0.1} = 140 \text{ mm} \]

Exercise 6.10

Groundwater flows horizontally from point A to point B. The difference in hydraulic head between point A and B is 1 meter, and the distance between point A and B is 1000 meters. The permeability of the soil is 10 m/d, and the porosity is 0.16.

a) Calculate the specific discharge from point A to point B.

b) On average, how many days does a water particle take to flow from point A to point B?

Consider now two channels with an equal water level. The average \(k_d\) of the subsurface is 95 m\(^2\)/day. The distance between the two channels is 90 meters. The groundwater recharge is 1 mm/day.

c) Calculate the groundwater bulging in the middle of the area.

Answer Exercise 6.10a

The specific discharge can be computed using Darcy’s law.

\[ q_x = K \frac{h_A -h_B}{L} = 10 \cdot \frac{1}{1000} = 0.01 \text{ m/d} \]

Answer Exercise 6.10b

The average velocity \(\overrightarrow{v}\) can be computed by dividing the specific discharge by the porosity.

\[ \overrightarrow{v} = \frac{\overrightarrow{q}}{n} = \frac{0.01}{0.16} = 0.0625 \text{ m/d} \]

So, a water particle needs on average \(\frac{1000}{0.0625}=16000\) days.

Answer Exercise 6.10c

The hydraulic head between the two canals can be computed using Hooghoudt’s equation:

\[ h = -\frac{N}{2KD}x^2 + (\frac{N}{2KD}L + \frac{h_2 - h_1}{L})x + h_1 \]

When the two canals have an equal groundwater level, then the groundwater level halfway the canals is:

\[ h_{\frac{1}{2}L} = h + \frac{NL^2}{8KD} = h + \frac{1 \cdot 10^{-3} \cdot 90^2}{8 \cdot 95} = h + 0.01066 \text{ m} \]

Then the bulging is equal to 10.66 mm.

Exercise 6.11

The figure shows a piezometer. The filter of this tube is positioned at a depth of -13 meters NAP. The piezometric level in the tube is -2 meters NAP. The pressure is measured with the pressure gauge 6 meters below the water level in the piezometer. The specific weight of water is 9.8 kN/m\(^3\).

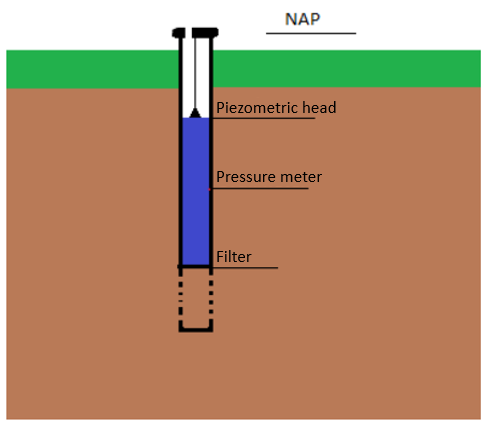
Fig. 6.26 Piezometer in the ground.

a) What is the pressure head at the depth of the filter?

b) How high is the pressure compared to atmospheric pressure at the pressure gauge?

A piezometer is positioned 1000m from a long straight river. Twelve days after the river level has risen by 1 meter, the piezometric level in the piezometer has increased by 0.2 meters.

c) How many days does it take for the piezometric level to rise by 0.2 meters in a piezometer located 500 meters from the river?

Answer Exercise 6.11a

The hydraulic head is defined as the sum of the pressure head and elevation head:

\[ h = \frac{p}{\gamma} + Z \]

At the filter, the hydraulic head is -2 meters NAP, and the elevation head is -13 meters NAP. Hence, the pressure head must be equal to \(h - Z\) = -2 - (-13) = 11 meters.

Answer Exercise 6.11b

At the water level in the piezometer, the pressure is equal to atmospheric pressure. The pressure gauge is located 6 meters below the water level. The pressure increases over this depth by 6 \(\cdot\) 9.81 = 58.86 kPa.

Answer Exercise 6.11c

If at a distance \(x\) from the river, the piezometric level has increased by 0.2 meters at time \(t_1\), then it takes four times longer to obtain the same increase at a distance \(2x\). Conversely, it can be concluded that at half the distance \(x\), the increase is observed four times faster. Hence, it takes 3 days for the piezometric level to rise by 0.2 meters in a piezometer located 500 meters from the river.

Exercise 6.12

Groundwater seeps into a polder through a clay layer with a resistance of 1.3 * 10\(^3\) days. The hydraulic head beneath the clay layer is +2 meters relative to NAP, while the water level in the polder is -1 meter relative to NAP. The surface area of the polder is 2.2 km\(^2\).

How many cubic meters of water seep into the polder per day?

Answer Exercise 6.12

The vertical flow through an aquitard can be described by the formula:

\[ q_z = \frac{h_2 - h_1}{c} \]

​

Where c represents the resistance of the clay layer, and h2 and h1 denote the hydraulic heads in the lower and upper aquifers.

Substituting the values:

\[ q_z = \frac{2-(-1)}{1.3 \cdot 10^{3}} = 2.31 \cdot 10^{-3} \text{ m/day} \]

Total seepage into the polder:

\[ 2.31 \cdot 10^{-3} \cdot 2.2 \cdot 10^6 = 5082 \text{ m$^3$/day} \]

Exercise 6.13

An aquifer is bounded by two long, deep rivers. The distance between the rivers is \(L\). There is no groundwater recharge because the aquifer is sealed with a clay layer with high hydraulic resistance. The water level in the river on the left is equal to \(h_1\) and on the right is equal to \(h_2\). The permeability of the aquifer is \(k\). The saturated thickness \(D\) of the aquifer can be considered constant. Groundwater flow in the aquifer is stationary and one-dimensional. A cross-section of the aquifer is shown in the figure below. The origin of the x-axis is chosen as indicated.

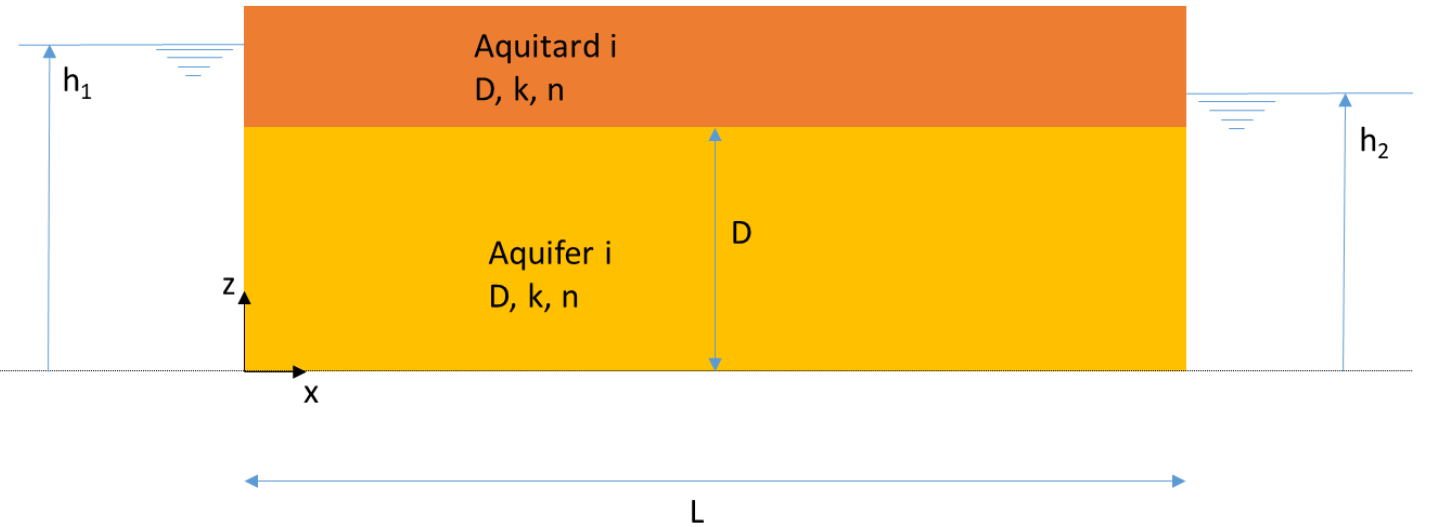
The following is known:

\(k_i\) = 15 m/d, \(D_i\) = 6 m, \(h_1\) = 8 m, \(h_2\) = 6 m, \(L\) = 800 m.

What is the specific discharge through the aquifer from the left to the right river?

Answer Exercise 6.13

The specific discharge through the aquifer from the left to the right can be computed using Darcy’s law.

\[ q= k_i \cdot \frac{h_1 -h_2}{L} = 15 \cdot \frac{2}{800} = 0.038 [m/d] \]

Exercise 6.14

We now also consider the underlying aquitard and aquifer, both of which extend far on either side of both rivers. The following additional data are known:

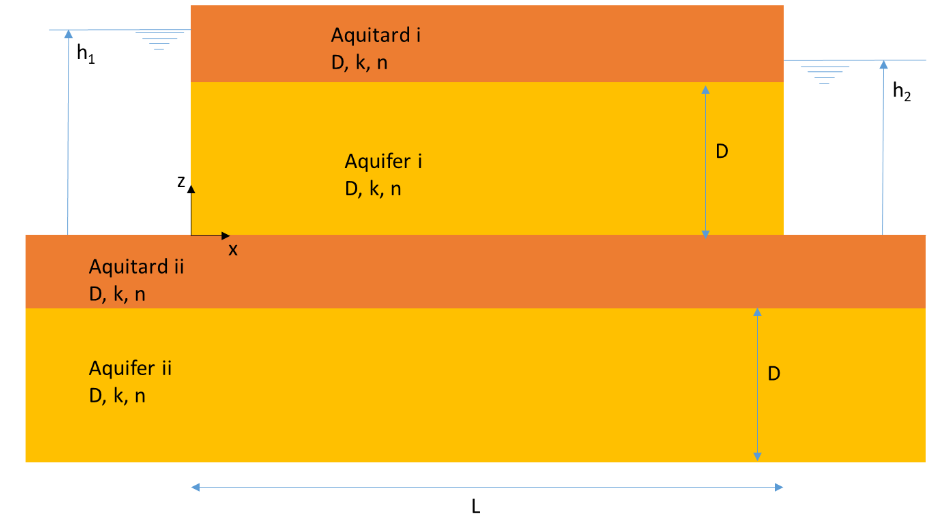
The following (new data) is known: \(D_{aquitard-ii}\) = 25 m, \(D_{aquifer-ii}\) = 40 m, \(k_{aquitard-ii}\) = 0.02 m/d, \(k_{aquifer-ii}\) = 20 m/d.

The following data from the previous exercise can be used: \(k_i\) = 15 m/d, \(D_i\) = 6 m, \(h_1\) = 8 m, \(h_2\) = 6 m, \(L\) = 800 m.

A) What is the hydraulic resistance of Aquitard ii? B) What is the leakage factor \(\lambda\) in Aquifer ii?

Answer Exercise 6.14a

A) The hydraulic resistance of the Aquitard:

\[ c_{aquitard} = \frac{D_{aquitard-ii}}{k_{aquitard-ii}} = \frac{25}{0.02} = 1250 d \]

Answer Exercise 6.14b

B) The leakage factor \(\lambda\) of Aquifer:

\[ \lambda = \sqrt{{D_{aquifer-ii}} \cdot {k_{aquifer-ii}} \cdot{c_{aquitard-ii}}} = \sqrt{{40} \cdot {20} \cdot{1250}} = 1000 m \]

Exercise 6.15

The water in Aquifer ii is fresh. Drinking water is extracted from this aquifer with a flow rate Q. The hydraulic head at a large distance from the extraction point in Aquifer ii can be considered uniform and is \(h_{ii}\) = 7 m.

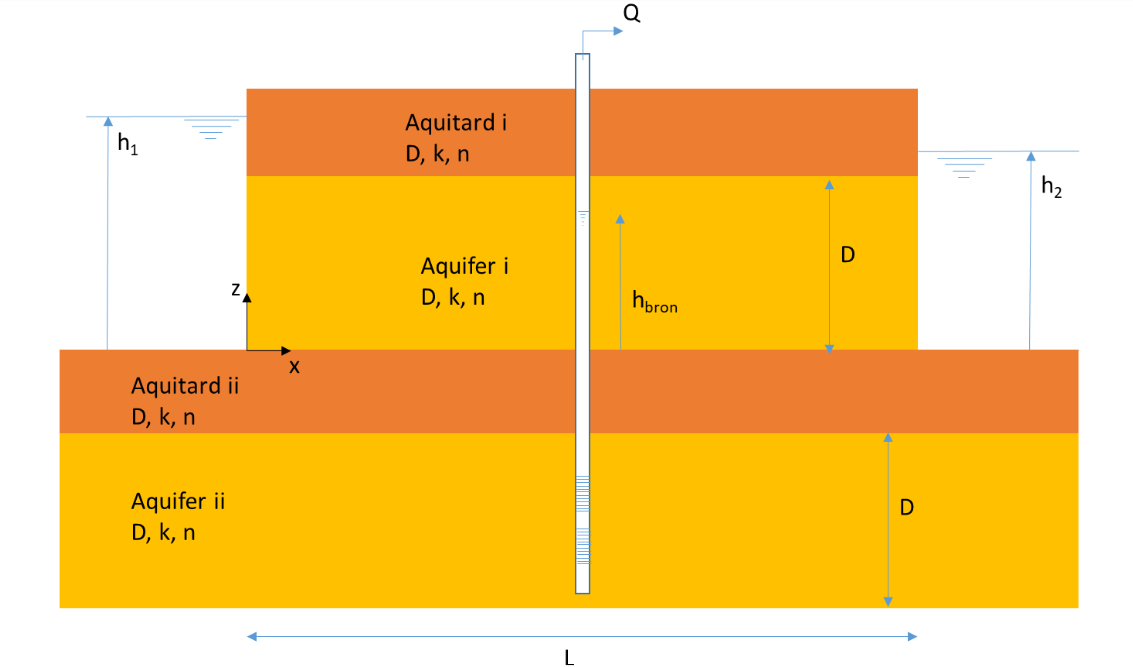
The following (new data) is known: \(h_{ii}\) = 7 m, \(Q\) = 50 m\(^3\)/h, \(r_{bron}\) = 0.25 m, \(\lambda\) = 1100 m (leakage factor, be aware don’t use the leakage factor calculated at the previous exercise).

The following data from the previous exercise can be used: \(D_{aquitard-ii}\) = 25 m, \(D_{aquifer-ii}\) = 40 m, \(k_{aquitard-ii}\) = 0.02 m/d, \(k_{aquifer-ii}\) = 20 m/d, \(k_i\) = 15 m/d, \(D_i\) = 6 m, \(h_1\) = 8 m, \(h_2\) = 6 m, \(L\) = 800 m.

A) What is the hydraulic head in the well? (Tip: Use for R the distance from the well where the hydraulic head \(h_{ii}\) is 3x the leakage factor.)

B) What is the specific discharge through (in the vertical direction) Aquitard ii directly next to the well? For calculating the hydraulic head difference between Aquifer i and Aquifer ii at the well, assume a linear hydraulic head gradient in Aquifer i.

Answer Exercise 6.15a

A) The hydraulic head in the well:

\[ Q = 50 \text{m$^3$/h} = 24 \cdot 50 = 1200 \text{m$^3$/d} R = \lambda \cdot 3 = 1100 * 3 = 3300 m \]

The hydraulic head in the well:

\[ H = h_{ii} - \frac{Q}{2 \pi k_{aquifer-ii} D_{aquifer-ii}} \ln \frac{R}{r_{bron}} H = 7 - \frac{1200}{2 \cdot \pi \cdot 20 \cdot 40} \ln \frac{R}{r_{bron}} = 4.73 m \]

Answer Exercise 6.15b

B) The specific discharge through (in the vertical direction) Aquitard ii directly next to the well: First calculate the h in the middle of the Aquifer i:

\[ h_{middle} = h_1 - (\frac{h_1-h_2}{L}\cdot 0.5 \cdot L) = 8 - (\frac{8-6}{800}\cdot 0.5 \cdot 800) = 7 \]

\[ dh = h_{middle} - h_{bron} = 7 - 4.73 = 2.27 m \]

\[ i = \frac{dh}{D_{aquitard-ii}} = \frac{2.27}{25} = 0.0908 [-] \]

\[ q_{aquitard-ii} = i \cdot k_{aquitard-ii} = 0.0908 \cdot 0.02 = 0.0018 m/d \]

Exercise 6.16

Due to the presence of a factory discharging wastewater containing PFAS into the river, water with PFAS also flows into the upper aquifer (Aquifer i). PFAS does not degrade and does not adhere to soil particles.

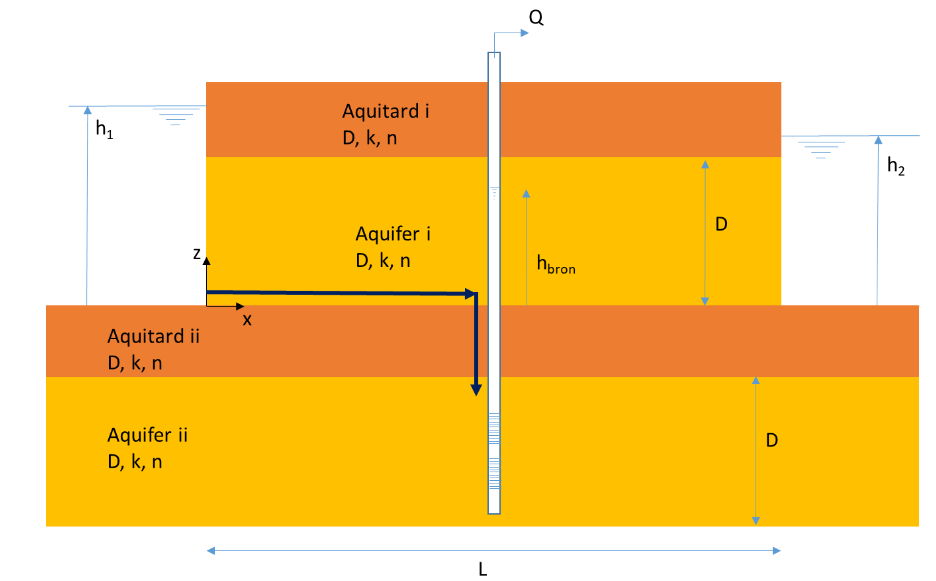
The following (new data) is known: Porosity is everywhere \(n\) = 0.3 [-]

Use the specific discharge \(q_{aquifer-i}\) = 0.041 The following data from the previous exercise can be used: \(D_{aquitard-ii}\) = 25 m, \(D_{aquifer-ii}\) = 40 m, \(k_{aquitard-ii}\) = 0.02 m/d, \(k_{aquifer-ii}\) = 20 m/d, \(k_i\) = 15 m/d, \(D_i\) = 6 m, \(h_1\) = 8 m, \(h_2\) = 6 m, \(L\) = 800 m.

After how much time can the PFAS be observed in the extraction at the earliest? The fastest path for a water droplet (with PFAS) from the left river to the well is indicated in the figure.

First, calculate how long it takes for the water to reach the well using the specific discharge in Aquifer i. Then calculate how long it takes to move through the aquifer using the specific discharge at the well.

Answer Exercise 6.16

\[ x_{aquifer-i} = \frac{L}{2} + \frac{800}{2} = 400 m \]

Calculate the speed of the groundwater in Aquifer i:

\[ v_{aquifer} = \frac{q_{aquifer-i}}{n} = \frac{0.041}{0.3} = 0.14 m/d \]

\[ t_{aquifer-i} = \frac{x_{aquifer-i}}{v_{aquifer}} = \frac{400}{0.14} = 2927 d \]

\[ x_{aquitard-ii} = D_{aquitard-ii} = 25 m \]

Calculate the speed of the groundwater, use the q_{aquitard_ii} from the previous question:

\[ v_{aquitard} = \frac{q_{aquitard-ii}}{n} = \frac{0.0018}{0.3} = 0.006040231 m/d \]

\[ t_{aquitard-ii} = \frac{x_{aquitard-ii}}{v_{aquitard}} = \frac{25}{0.006} = 4139 d \]

\[ t_{total} = t_{aquifer-i} + t_{aquitard-ii} = 2927 + 4139 = 7066 d \]