2.2. Water balance

Hydrologists work with open systems whose boundaries are often chosen as the boundaries of a catchment area. The water in the hydrological cycle can be quantified with simple mass balances. The change in storage is equal to the difference between the incoming and outgoing fluxes. The water balance is based on the conservation of mass. However, in practice, volumes are used instead of masses. The water balance formula reads:

(2.1)\[ {\text{d}S \over \text{d}t} = Q_\text{in}-Q_\text{out} \quad \text{[L$^{3}$/T]} \]

With:

\(S\)	Storage	\({[\mathrm{L}^{3}]}\)
\(Q_\text{in}\)	Incoming fluxes	[\(\mathrm{L}^{3}/\mathrm{T}\)]
\(Q_\text{out}\)	Outgoing fluxes	[\(\mathrm{L}^{3}/\mathrm{T}\)]

In most catchment areas, such as rivers, \(Q_\text{in}\) and \(Q_\text{out}\) consist of the following components:

(2.2)\[ Q_\text{in}=PA \hspace{40pt} \& \hspace{40pt} Q_\text{out}=EA + Q \hspace{40pt} \text{[$\mathrm{L}^{3}/\mathrm{T}$]} \]

With:

\(P\)	Intensity of precipitation	\({[\mathrm{L}/\mathrm{T}]}\)
\(A\)	Area	\({[\mathrm{L}^{2}]}\)
\(E\)	Evaporation	[\(\mathrm{L}/\mathrm{T}\)]
\(Q\)	River discharge	[\(\mathrm{L}^{3}/\mathrm{T}\)]

Evaporation and storage differ for land and open water, therefore a distinction is made:

(2.3)\[ A = A_\text{s} + A_\text{w} \hspace{50pt} \text{[L$^{2}]$} \]

With:

\(A_\text{s}\)	Area of land surface	\([\mathrm{L}^{2}]\)
\(A_\text{w}\)	Area of surface water	\([\mathrm{L}^{2}]\)

The total evaporation consists of four terms:

(2.4)\[ E=E_\text{i}+E_\text{t}+E_\text{s}+E_\text{o} \hspace{50pt} \text{[L/T]} \]

With:

\(E_\text{i}\)	Interception	[L/T]
\(E_\text{t}\)	Transpiration	[L/T]
\(E_\text{s}\)	Soil evaporation	[L/T]
\(E_\text{o}\)	Open water evaporation	[L/T]

Intercepted water evaporates from the surface shortly after precipitation has fallen (within one or two days, often faster). Transpiration can be referred to as evaporation that takes place from the rootzone through the stomata (NL: huidmondjes) in the leaves of vegetation. Soil evaporation also occurs from the unsaturated zone but through the pores between the soil particles. Open water evaporation is evaporation from the open water surface storage. The total storage consists therefore of four components:

(2.5)\[ S=S_\text{s}+S_\text{u}+S_\text{g}+S_\text{w} \hspace{50pt} \text{[L$^3$]} \]

With:

\(S_\text{s}\)	Storage on the land surface	\([\mathrm{L}^{3}]\)
\(S_\text{u}\)	Storage in the soil (soil moisture in the unsaturated zone)	\([\mathrm{L}^{3}]\)
\(S_\text{g}\)	Storage in saturated zone (groundwater)	\([\mathrm{L}^{3}]\)
\(S_\text{w}\)	Storage in open water	\([\mathrm{L}^{3}]\)

Sub-balances can be made from the mentioned storage components. Fig. 2.4 shows all the storage elements and fluxes between the components. The dotted frames represent the system boundaries of the sub-areas.

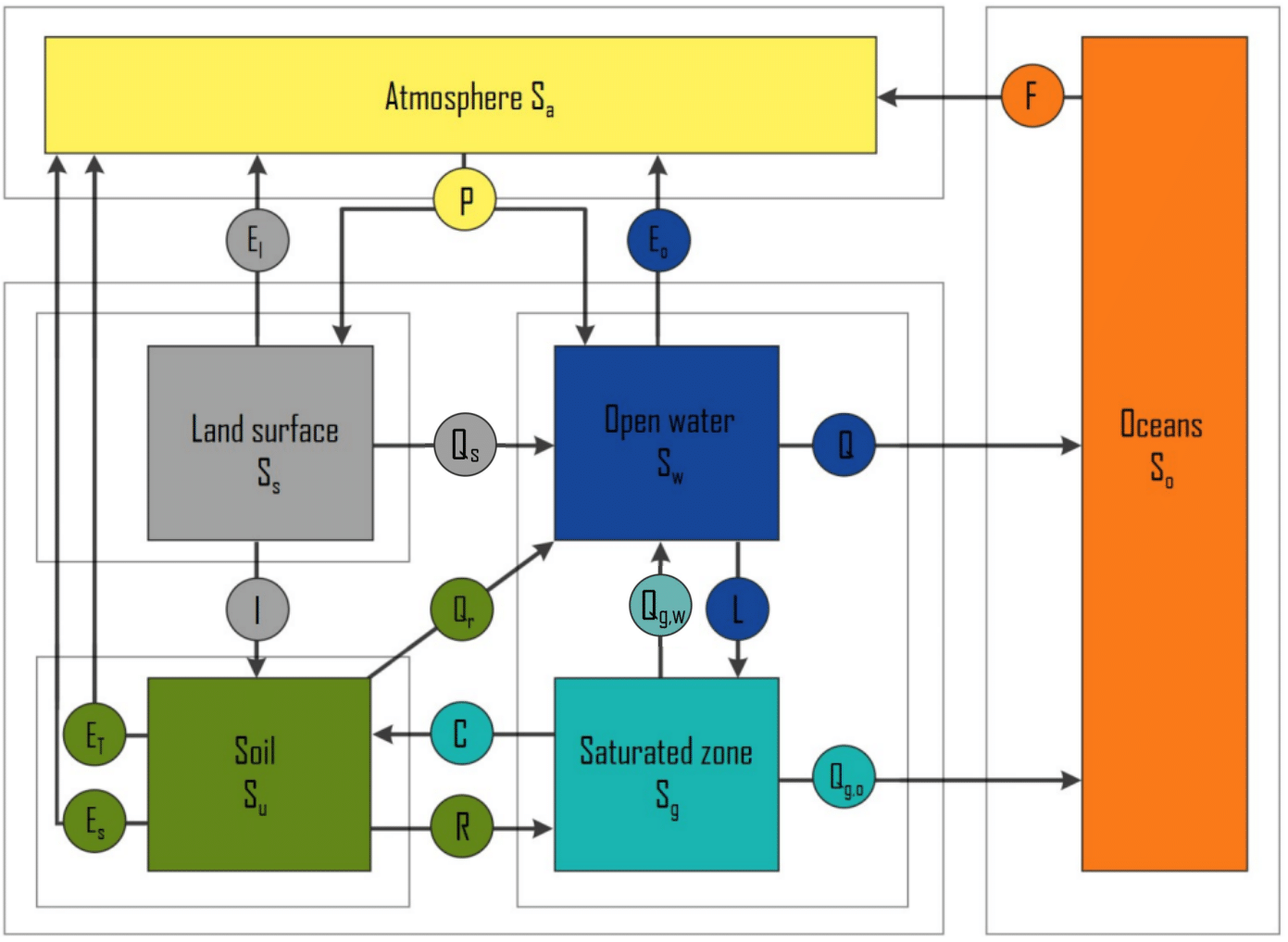
Fig. 2.4 Fluxes and storages of the water balance between different subareas. Fluxes are given as circles, storage components as boxes.(Own work)

From the elements in the formula of the water balance and Fig. 2.4 various sub-balances can be made. These are global water balances but in principle a water balance can be established for each small or large system area.

• Partial balance surface area

(2.6)\[ {\text{d}S_\text{s} \over \text{d}t} = (P-E_\text{i}-I)A_\text{s}-Q_\text{s} \quad \text{[L$^{3}$/T]} \]

With:

\(I\)	Infiltration into unsaturated zone	[L\(^{3}\)/T]
\(Q_\text{s}\)	Surface flow to open water	[L\(^{3}\)/T]

• Partial balance soil

(2.7)\[ {\text{d}S_\text{u} \over \text{d}t} = (I+C-E_\text{t}-E_\text{s}-R)A_\text{s}-Q_\text{r} \quad \text{[L$^{3}$/T]} \]

With:

\(C\)	Capillary rise	[L/T]
\(R\)	Recharge	[L/T]
\(Q_\text{r}\)	Rapid runoff through the soil	[L\(^{3}\)/T]

• Partial balance renewable groundwater

(2.8)\[ {\text{d}S_\text{g} \over \text{d}t} = (R-C)A_\text{s}+LA_\text{w}-Q_\text{g,o}-Q_\text{g,w} \quad \text{[L$^{3}$/T]} \]

With:

\(L\)	Leakage	[L/T]
\(Q_\text{g,o}\)	Subsurface runoff to sea or ocean	[L\(^{3}\)/T]
\(Q_\text{g,w}\)	Subsurface runoff to open water	[L\(^{3}\)/T]

• Partial balance open water

(2.9)\[ {\text{d}S_\text{w} \over \text{d}t} = (P-E_\text{o}-L)A_\text{w}+Q_\text{s}+Q_r+Q_\text{g,w}-Q \quad \text{[L$^{3}$/T]} \]

With:

\(Q\)	Discharge of river(s)	[L\(^{3}\)/T]

• Total water balance

(2.10)\[ {\text{d}(S_\text{s}+S_\text{u}+S_\text{g}+S_\text{w}) \over \text{d}t} = (P-E_\text{i}-E_\text{t}-E_\text{s})A_\text{s}+(P-E_\text{o})A_\text{w}-Q-Q_\text{g,o} \quad \text{[L$^{3}$/T]} \]

The total water balance does not contain all the terms which are included in the partial balances. These terms are internal fluxes of the total system area and cause no change in the total storage. However, for the storage subsystems, these internal fluxes are important. Fig. 2.4 also shows two compartments and a flux which are not included in the partial balances or total balance of the land compartment at all. The reason is that these elements (oceans, atmosphere and evaporation from the ocean to the atmosphere) are not part of the terrestrial compartment.

For the ocean and the atmosphere, the water balances are respectively:

(2.11)\[ {\text{d}S_\text{o} \over \text{d}t} = Q+Q_{g,o}-F \quad \text{[L$^{3}$/T]} \]

(2.12)\[ {\text{d}S_\text{a} \over \text{d}t} = (E_\text{i}+E_\text{t}+E_\text{s})A_\text{s}+E_\text{o}A_\text{w}+F-P \quad \text{[L$^{3}$/T]} \]

With:

\(F\)	Net flux from ocean to atmosphere	[L\(^{3}\)/T]

These fluxes are shown in Fig. 2.4 because they make the water cycle complete and they belong to the earth system.

2.2.1. System boundary

A water balance can be determined if the the various terms can be quantified. The first step is to define the system boundary, which determines the terms which should be taken into account in the water balance and the terms which can be neglected.

The system boundary for the total water balance is often chosen close to the land surface. The precipitation reaching the land surface and evaporation from the land surface are easier to determine than the amounts of water vapor entering and leaving the atmosphere. Furthermore, the amount of water in the atmosphere is difficult to determine properly.

The system boundary can be different for different sub-water balances. For example, a river basin is bounded by a divide (NL: waterscheiding) defined by topography. This watershed determines the flow direction. The system boundary of groundwater systems is not necessarily determined by topography as shown in Fig. 2.5. Water infiltrated at one side of the topographic divide (A) can flow through an aquifer towards the other side of the topographic divide (B).

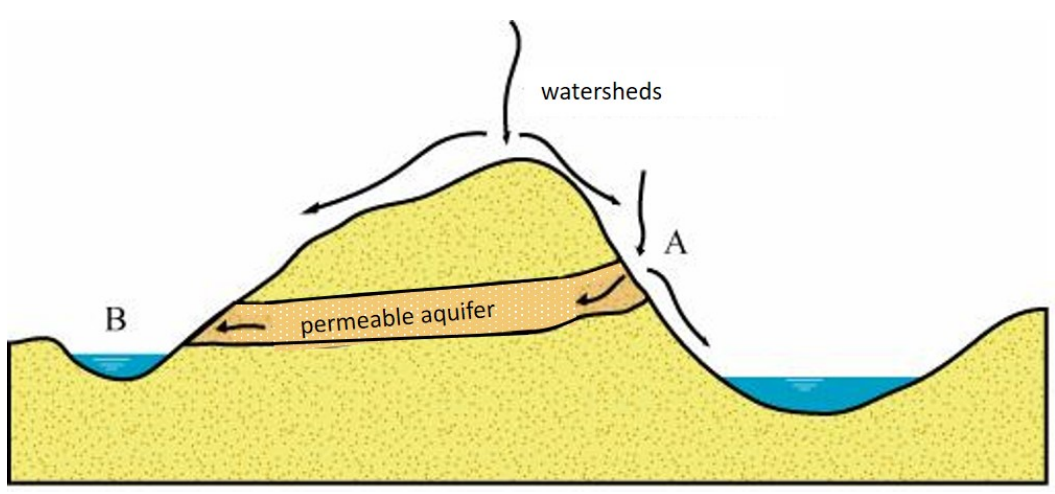
Fig. 2.5 Surface water divide and groundwater divide.

2.2.2. Human factors

The water balance does not necessarily need to consist only of natural factors; often human interventions such as ground and surface water extraction affect the natural balance. A good example of this is a polder. Polders can be thought of as unique catchment areas. The inflow and outflow of water is artificially controlled with weirs (NL: overlaten) and/or pumping stations. Due to the polder’s low altitude, groundwater can flow in from surrounding areas and seep into the polder. Therefore, in addition to the natural terms a number of human intervention terms must be added to the water balance. Obviously, the influence of human interventions on the water balance decreases when the size of the system under consideration increases.

2.2.3. Time influence

It is important to choose the correct time scale when drawing up a water balance and working with it. By choosing a longer time scale, the inflow and outflow quantities of the system will increase. However, the change in storage will both increase and decrease. In the long term, the influence of the change of storage will become limited be little. By taking a time period of several years the change of storage can be assumed negligible.

# Note that the code cells below is used for the website only.

Exercise 2.1

From a watershed, the following data has been collected:

• Average annual precipitation = 800 mm/year

• Average annual discharge = 3.0 m\(^3\)/s

• Area = 432 km\(^2\).

The topographic divide corresponds to the groundwater divide.

a) Determine the average annual evaporation \(E\) in mm/year.

A reservoir is being constructed in the watershed. The estimated average annual evaporation \(E_o\) from the reservoir is 1181 mm/year. After the reservoir’s construction, the average annual discharge from the watershed is found to be 2.8 m\(^3\)/s.

b) Determine the area of the reservoir.

Answer Exercise 2.1a

Since we’re looking at an annual basis, we can assume storage change \(\frac{\text{d}S}{\text{d}t} = 0\). Thus, we have: \(\frac{\text{d}S}{\text{d}t} = PA - EA - Q = 0\), which leads to:

\[ E = P - \frac{Q}{A} \quad [] \]

Substituting the given values, we get the evaporation value:

\[ E = 800 - \frac{3 \cdot 10^9 \cdot 3600 \cdot 24 \cdot 365}{432 \cdot 10^{12}} = 800 - 219 = 581 \: \text{mm/year}. \]

Answer Exercise 2.1b

Method 1

Since we’re looking at an annual basis again, we have

\[ \frac{\text{d}S}{\text{d}t} = P \cdot A - E \cdot A - Q = 0 \]

By splitting the terms, we get:

\[ P \cdot (A_s + A_w) - E_s \cdot A_s - E_o \cdot A_w - Q = 0 \]

Substituting the given values (in m\(^3\)/year), we get:

\[ \begin{align}\begin{aligned} (800 \cdot 10^{-3}) \cdot (432 \cdot 10^6)-(581\cdot10^{-3}) \cdot ((432 \cdot 10^6) - A_w) \\- (1181 \cdot 10^{-3}) \cdot A_w - 2.8\cdot3600\cdot24\cdot365=0 \end{aligned}\end{align} \]

which gives \(A_w=10.5\) km\(^2\).

Method 2

Another possibility is to calculate with the fact that the decrease in the discharge volume is equal is due to the increase in the volume of evaporation from the reservoir:

\[ 0.2 \cdot 3600 \cdot 24 \cdot 365 = A_w \cdot (1181 - 581) \cdot 10^{-3} \]

this calculation also results in \(A_w=10.5\) km\(^2\).

# Note that the code cells below is used for the website only.

Exercise 2.2

The following data have been collected for a river basin:

• Average annual precipitation = 1000 mm/year = 1 m/year

• Average annual evaporation = 500 mm/year = 0.5 m/year

• Area = 80 km\(^2\)

a) What is the total annual discharge from the river basin?

In the winter period (180 days), half of the yearly precipitation falls and 30% of the yearly evaporation occurs. During this period, the storage increased by 10 cm.

b) What is the average discharge in the winter period?

Answer Exercise 2.2a

\[ Q = A \cdot (P - E) = (80 \cdot 10^6) \cdot (1 - 0.5) = 40 \cdot 10^6 \: \text{m$^3$/year} \]

Answer Exercise 2.2b

\(P = 500 \: \text{mm}/\text{180 days} = 0.5 \: \text{m}/\text{180 days}\)

\(E = 0.3 \cdot 500 = 150 \: \text{mm}/\text{180 days} = 0.15 \: \text{m}/\text{180 days}\)

\(\frac{dS}{dt} = 10 \: \text{cm}/\text{180 days} = 0.10 \: \text{m}/\text{180 days}\)

From the water balance, it follows that:

\(Q=A \cdot (P-E-dS/dt)\)

\(Q=(80 \cdot 10^6) \cdot (0.5-0.14-0.10)=20 \cdot 10^6 \: \text{m}^3/\text{180 days}\)

\(Q=\frac{20 \cdot 10^6}{(180 \cdot 24 \cdot 3600)}=1.29 \: \text{m}^3/\text{s}\)