Learning and Model Selection

Up until now we have been assuming values for our hyperparameters \(\alpha\) and \(\beta\). Recall that the MAP solution is equivalent to an MLE model with \(L_2\) regularization term \(\lambda={\alpha}/{\beta}\), which suggests that \(\alpha\) and \(\beta\) control the flexibility of our model.

In an MLE approach, simply minimizing the loss function for \(\alpha\) and \(\beta\) would always result in the most flexible model possible, which is however prone to overfitting. In frequentist model selection we solve this dilemma by keeping some data aside as validation dataset and adopting the regularization parameter that miminizes the validation loss.

Bayesian models on the other hand tend to be more resistant to overfitting, and there is in principle no need to hold out some data when calibrating hyperparameters, as we will see in this page. We first set up this model selection problem in a probabilistic way.

Bayesian model selection

We have seen before that we can draw models with different \(\mathbf{w}\) from our posterior distribution. Now imagine a bag of models with not only different weights but different complexity, structures and assumptions. In practical engineering, different options could be e.g. simple analytical calculations, a Finite Differences model and a Finite Element Model. Let us assume for now that we have a discrete number of model choices \(\mathcal{M}_i\).

Because we are working in a Bayesian setting, it is elegant to also treat model choices \(\mathcal{M}_i\) in the same way. Adopting priors \(p(\mathcal{M}_i)\) for each choice of model, we can use Bayes’ Theorem to compute posteriors:

(63)\[ p(\mathcal{M}_i\vert\mathcal{D}) = \displaystyle \frac{p(\mathcal{M}_i)p(\mathcal{D}\vert\mathcal{M}_i)}{p(\mathcal{D})} \]

These posteriors probabilities provide an answer to the question given our observed data, which model is most likely to explain what we see? Once computed, we can follow the same approach we used to compute the predictive distribution \(p(\hat{t})\) by marginalizing over \(\mathbf{w}\) we can also do the same to average predictions coming from different models:

(64)\[ p(\hat{t}\vert\hat{\mathbf{x}},\mathcal{D}) = \displaystyle\sum_i^L p(\hat{t}\vert\hat{\mathbf{x}},\mathcal{M}_i,\mathcal{D}) p(\mathcal{M}_i\vert\mathcal{D}) \]

where averaging becomes a summation because \(\mathcal{M}\) is a discrete variable. The issue is that even if all conditionals \(p(\hat{t}\vert\hat{\mathbf{x}},\mathcal{D})\) are Gaussian, this average is a mixture of Gaussians and therefore not itself Gaussian.

Suppose we do not want to handle this non-Gaussianity, which is often the case. As always, it is possible to take a shortcut, and as we will see next it is a familiar one.

Empirical Bayes

Going back to Eq. (63), the second term in the numerator is the so-called model evidence, i.e. how likely the observed data is given the model. This takes the same role as the likelihood function \(p(\mathbf{t}\vert\mathbf{w})\) from before (Eq. (41)). At that point we could take a shortcut and just get \(\mathbf{w}\) that maximizes this likelihood (MLE).

So why not do the same here? To get to \(p(\mathcal{M}_i\vert\mathcal{D})\) we need to marginalize over \(\mathbf{w}\):

(65)\[ p(\mathcal{D}\vert\mathcal{M}_i)= \displaystyle\int p(\mathcal{D}\vert\mathcal{M}_i,\mathbf{w})p(\mathbf{w}\vert\mathcal{M}_i)\,\mathrm{d}\mathbf{w} \]

where we see that the only conditional left is the model \(\mathcal{M}_i\) itself. We therefore call this the marginal likelihood. In the spirit of MLE, the best possible model choice would be the one that maximizes this likelihood.

More concretely, we can further specify \(\mathcal{M}_i\) as models having different values for an arbitrary set of hyperparameters \(\mathbf{h}\). We can then formally define our goal:

Empirical Bayes (Type-2 Maximum Likelihood Estimation)

Given a marginal likelihood function \(p(\mathcal{D}\vert\mathbf{h})\) where model parameters \(\mathbf{w}\) have been marginalized but hyperparameters \(\mathbf{h}\) remain, compute \(\mathbf{h}\) that maximizes this function.

The crucial point here is that because of this marginalization over \(\mathbf{w}\), the likelihood of the most flexible model is usually not the highest and extra terms appear in \(p(\mathcal{D}\vert\mathcal{M}_i)\) that tend to penalize very flexible models. This means we do not necessarily need a validation set to learn something about \(\mathbf{h}\) and can therefore use our complete dataset for learning!

Further Reading

This subject is also treated in detail in Section 3.4 with a few additional insights.

bishop-prml

Back to basis function models

Coming back to our original setup with \(\mathbf{h}=[\alpha,\beta]\), our marginal likelihood is:

(66)\[ p(\mathbf{t}\vert\alpha,\beta) = \displaystyle\int p(\mathbf{t}\vert\mathbf{w},\beta)p(\mathbf{w}\vert\alpha) \,\mathrm{d}\mathbf{w} \]

where we omit \(\mathbf{X}\) for simplicity. Note how this is exactly the denominator of Bayes’ Theorem when we compute \(p(\mathbf{w}\vert\mathbf{t})\). We can therefore use the same standard expressions from before and compute the evidence as:

(67)\[ \ln p(\mathbf{t}\vert\alpha,\beta) = \displaystyle\frac{N}{2}\ln\beta -\frac{\beta}{2}\sum_{n=1}^{N}\left[t_n-\mathbf{m}_N^\mathrm{T}\boldsymbol{\phi}(\mathbf{x}_n)\right]^2 -\frac{\alpha}{2}\mathbf{m}_N^\mathrm{T}\mathbf{m}_N {\color{red} + \frac{M}{2}\ln\alpha - \frac{1}{2}\ln\vert\mathbf{S}_N\vert - \frac{N}{2}\ln(2\pi) } \]

where \(\mathbf{m}_N\) and \(\mathbf{S}_N\) come from the posterior \(p(\mathbf{w}\vert\mathbf{t})\) and we take the natural logarithm of the resulting distribution. The terms in red tend to penalize models that are too flexible. They are often referred to as Occam’s factor, in reference to the famous Occam’s Razor.

Note how Eq. (67) is now a function of only \(\alpha\) and \(\beta\). We can therefore use an optimization algorithm to find the values that maximize our model evidence.

The example below demonstrates this learning process for a dataset of 10 points fitted with 9 radial basis functions, with each plot showing different moments during the optimization procedure:

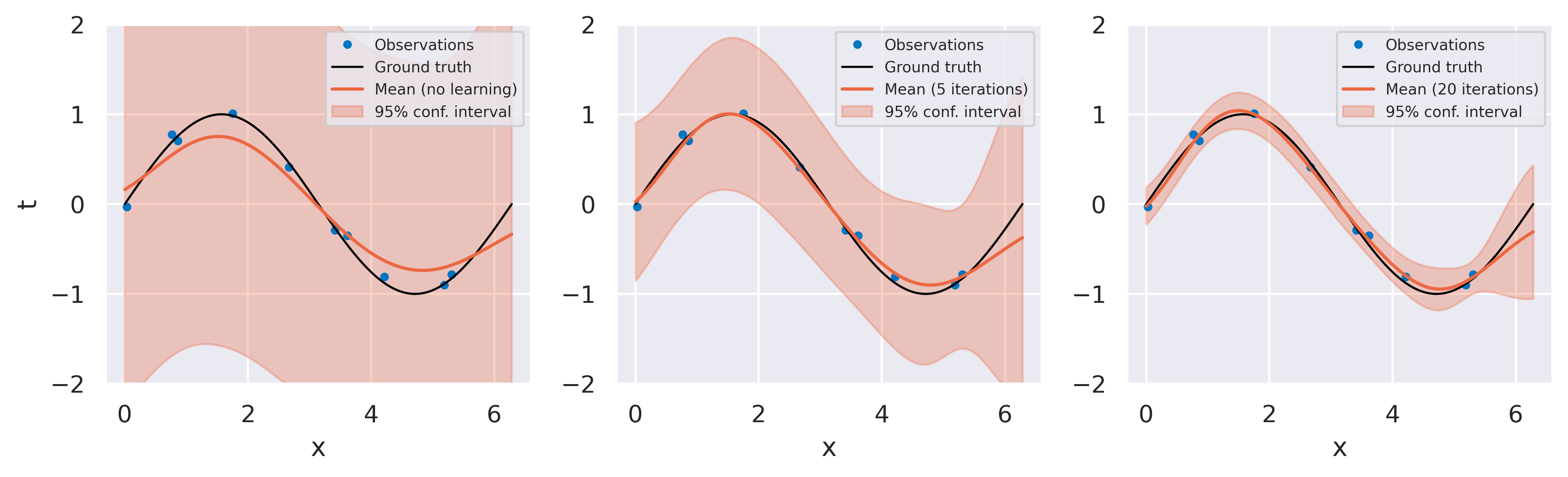
We can see how the initial values \(\alpha=\beta=1\) sacrifice too much flexibility for parsimony. After 20 iterations, the optimizer finds that the model with \(\alpha=4.4\) and \(\beta=175.9\) gives the highest value for the log marginal likelihood. Crucially, we could get to these values without sacrificing any of our data points to serve as validation data.