Solve influence line using ODE

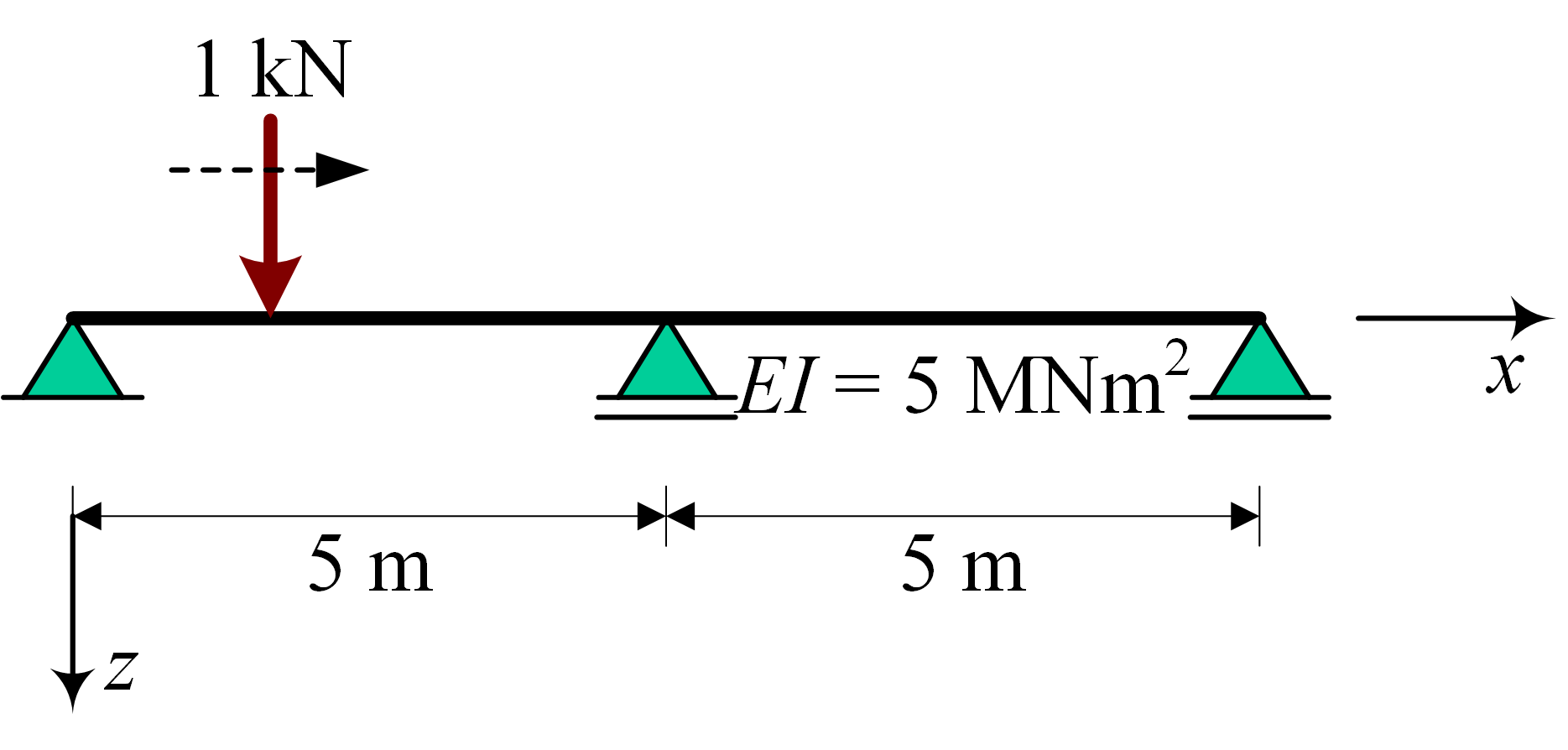
import sympy as sym
sym.init_printing()

x = sym.symbols('x')

EI = 5000

Find displacement line

q_BC = 0
q_AB = sym.SingularityFunction(x,3,-1)
display(q_AB)

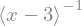
C_1, C_2, C_3, C_4, C_5, C_6, C_7, C_8 = sym.symbols('C_1, C_2, C_3, C_4, C_5, C_6, C_7, C_8')
V_AB = - sym.integrate(q_AB,x) + C_1
M_AB = sym.integrate(V_AB,x) + C_2
kappa_AB = M_AB / EI
phi_AB = sym.integrate(kappa_AB,x)+C_3
w_AB = - sym.integrate(phi_AB,x)+C_4
display(w_AB)

V_BC = - sym.integrate(q_BC,x) + C_5
M_BC = sym.integrate(V_BC,x) + C_6
kappa_BC = M_BC / EI
phi_BC = sym.integrate(kappa_BC,x)+C_7
w_BC = - sym.integrate(phi_BC,x)+C_8
display(w_BC)

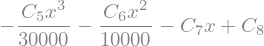
eq1 = sym.Eq(w_AB.subs(x,0),0)
eq2 = sym.Eq(M_AB.subs(x,0),0)
eq3 = sym.Eq(w_AB.subs(x,5),0)
eq4 = sym.Eq(w_BC.subs(x,5),0)
eq5 = sym.Eq(M_AB.subs(x,5),M_BC.subs(x,5))
eq6 = sym.Eq(phi_AB.subs(x,5),phi_BC.subs(x,5))
eq7 = sym.Eq(w_BC.subs(x,10),0)
eq8 = sym.Eq(M_BC.subs(x,10),0)

sol = sym.solve([eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8],[C_1, C_2, C_3, C_4, C_5, C_6, C_7, C_8])
display(sol)

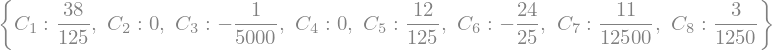
w_sol_AB = w_AB.subs(sol)
display(w_sol_AB)

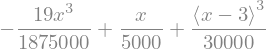
w_sol_BC = w_BC.subs(sol)
display(w_sol_BC)

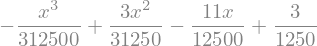
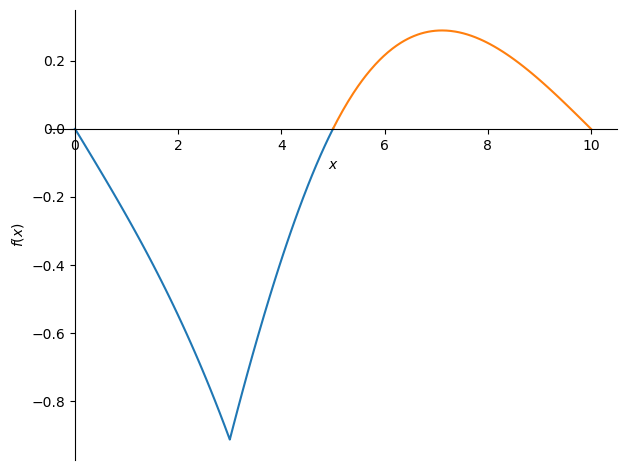
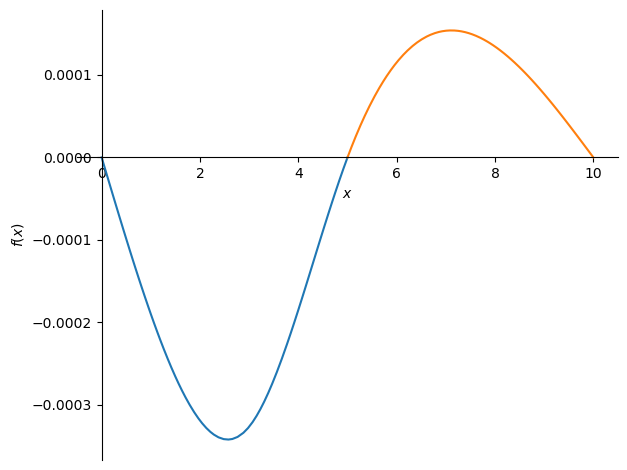
sym.plot((-w_sol_AB,(x,0,5)),(-w_sol_BC,(x,5,10)));

Find influence lines \(A_v\)

q_BC = 0
q_AB = 0
display(q_AB)

V_AB = - sym.integrate(q_AB,x) + C_1
M_AB = sym.integrate(V_AB,x) + C_2
kappa_AB = M_AB / EI
phi_AB = sym.integrate(kappa_AB,x)+C_3
w_AB = - sym.integrate(phi_AB,x)+C_4

eq1 = sym.Eq(w_AB.subs(x,0),1)

sol = sym.solve([eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8],[C_1, C_2, C_3, C_4, C_5, C_6, C_7, C_8])

w_sol_AB = w_AB.subs(sol)
w_sol_BC = w_BC.subs(sol)

sym.plot((-w_sol_AB,(x,0,5)),(-w_sol_BC,(x,5,10)));

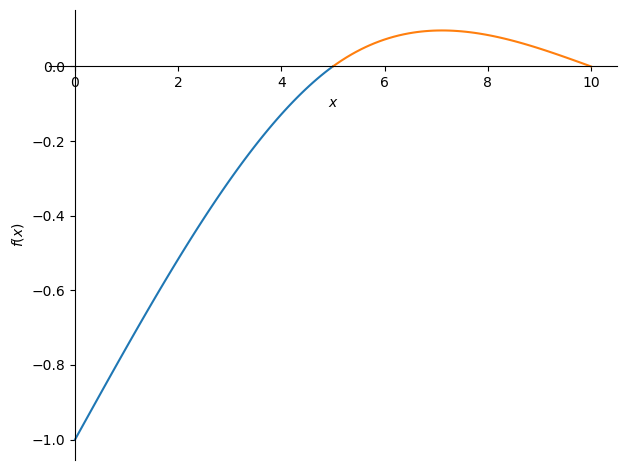
Find influence line \(V\) for \(x= 5^{-}\)

w_AB = - sym.integrate(phi_AB,x)+C_4 + sym.SingularityFunction(x,4.9999,0)
display(w_AB)

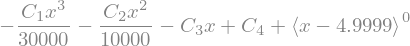
eq1 = sym.Eq(w_AB.subs(x,0),0)
eq2 = sym.Eq(M_AB.subs(x,0),0)
eq3 = sym.Eq(w_AB.subs(x,5),0)
eq4 = sym.Eq(w_BC.subs(x,5),0)
eq5 = sym.Eq(M_AB.subs(x,5),M_BC.subs(x,5))
eq6 = sym.Eq(phi_AB.subs(x,5),phi_BC.subs(x,5))
eq7 = sym.Eq(w_BC.subs(x,10),0)
eq8 = sym.Eq(M_BC.subs(x,10),0)

sol = sym.solve([eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8],[C_1, C_2, C_3, C_4, C_5, C_6, C_7, C_8])

w_sol_AB = w_AB.subs(sol)
w_sol_BC = w_BC.subs(sol)

sym.plot((-w_sol_AB,(x,0,5)),(-w_sol_BC,(x,5,10)));

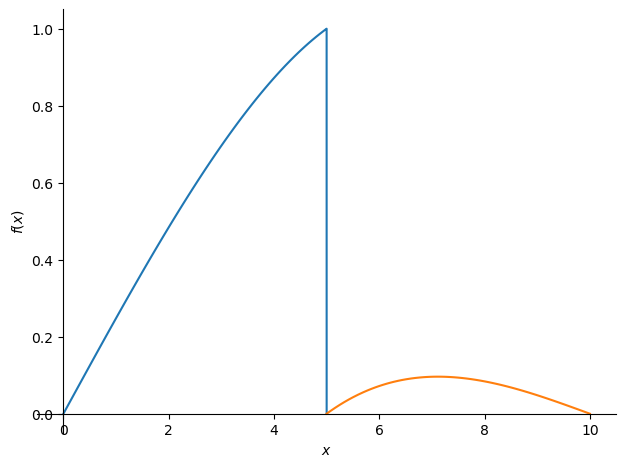
Find influence line \(M\) for \(x = 3\)

q_AB = 0
q_BC = 0
V_AB = -sym.integrate(q_AB,x)+C_1
M_AB = sym.integrate(V_AB,x)+C_2
kappa_AB = M_AB/ EI
phi_AB = sym.integrate(kappa_AB,x)+C_3 + sym.SingularityFunction(x,3,0)
display(phi_AB)
w_AB = sym.integrate(phi_AB,x)+C_4

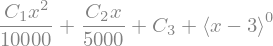
V_BC = -sym.integrate(q_BC,x)+C_5
M_BC = sym.integrate(V_BC,x)+C_6
kappa_BC = M_BC/EI
phi_BC = sym.integrate(kappa_BC,x) + C_7
w_BC = sym.integrate(phi_BC,x) + C_8

eq1 = sym.Eq(w_AB.subs(x,0),0)
eq2 = sym.Eq(M_AB.subs(x,0),0)
eq3 = sym.Eq(w_AB.subs(x,5),0)
eq4 = sym.Eq(w_BC.subs(x,5),0)
eq5 = sym.Eq(M_AB.subs(x,5),M_BC.subs(x,5))
eq6 = sym.Eq(phi_AB.subs(x,5),phi_BC.subs(x,5))
eq7 = sym.Eq(w_BC.subs(x,10),0)
eq8 = sym.Eq(M_BC.subs(x,10),0)

sol = sym.solve([eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8],[C_1,C_2,C_3,C_4,C_5,C_6,C_7,C_8])

w_AB_sol = w_AB.subs(sol)
w_BC_sol = w_BC.subs(sol)

sym.plot((w_AB_sol,(x,0,5)),((w_BC_sol),(x,5,10)));