Principle of minimum total potential energy with trial function

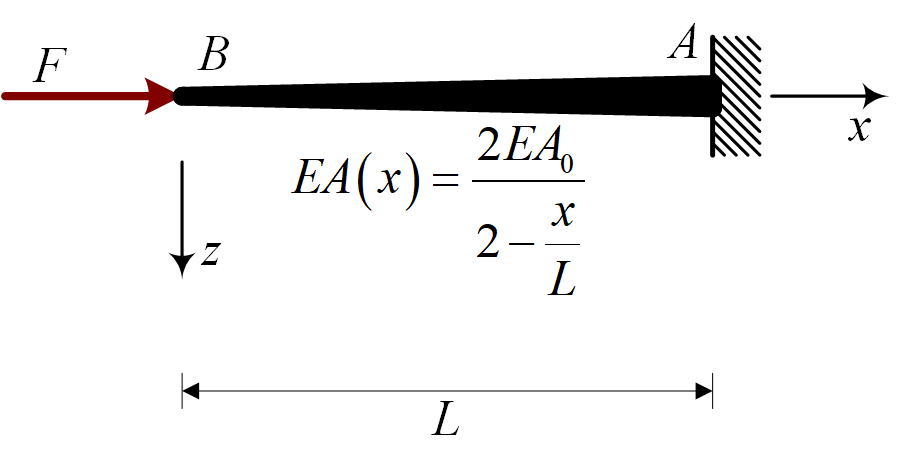
Solving use trial function

With trial function:

import sympy as sym
EA_0, a, x, L, F = sym.symbols('EA_0, a, x, L, F')
EA = 2 * EA_0 / (2 - x / L)
u_trial = a * (1 - x / L)
display(u_trial)

\[\displaystyle a \left(1 - \frac{x}{L}\right)\]

And strain energy:

eps_trial = u_trial.diff(x)
Ev = sym.simplify(sym.integrate( EA * eps_trial**2 / 2,(x,0,L)))
display(Ev)

\[\displaystyle \frac{EA_{0} a^{2} \log{\left(2 \right)}}{L}\]

And total potential energy:

V = Ev  - F * u_trial.subs(x,0)
display(V)
eq1 = sym.Eq(sym.diff(V,a),0)

\[\displaystyle \frac{EA_{0} a^{2} \log{\left(2 \right)}}{L} - F a\]

Solving for \(a\) gives:

a_sol = sym.solve(eq1,a)[0]
u_trial_subs = u_trial.subs(a,a_sol)
display(u_trial_subs)

\[\displaystyle \frac{F L \left(1 - \frac{x}{L}\right)}{2 EA_{0} \log{\left(2 \right)}}\]

Solving with ODE

u = sym.Function('u')
EA = 2 * EA_0 / (2 - x / L)

The ODE is defined as:

DV = sym.Eq((EA*u(x).diff(x)).diff(x),0)
display(DV)

\[\displaystyle \frac{2 EA_{0} \frac{d^{2}}{d x^{2}} u{\left(x \right)}}{2 - \frac{x}{L}} + \frac{2 EA_{0} \frac{d}{d x} u{\left(x \right)}}{L \left(2 - \frac{x}{L}\right)^{2}} = 0\]

The general solution of this ODE is:

C1, C2 = sym.symbols('C1, C2')
u_sol = sym.dsolve(DV,u(x)).rhs
display(u_sol)

\[\displaystyle C_{1} + 2 C_{2} L x - \frac{C_{2} x^{2}}{2}\]

Solving for the boundary conditions gives:

eps = u_sol.diff(x)
N = EA * eps
eq1 = sym.Eq(N.subs(x,0),-F)
eq2 = sym.Eq(u_sol.subs(x,L),0)
sol = sym.solve((eq1,eq2),(C1,C2))
u_subs = u_sol.subs(sol)
display(u_subs)

\[\displaystyle \frac{3 F L}{4 EA_{0}} - \frac{F x}{EA_{0}} + \frac{F x^{2}}{4 EA_{0} L}\]

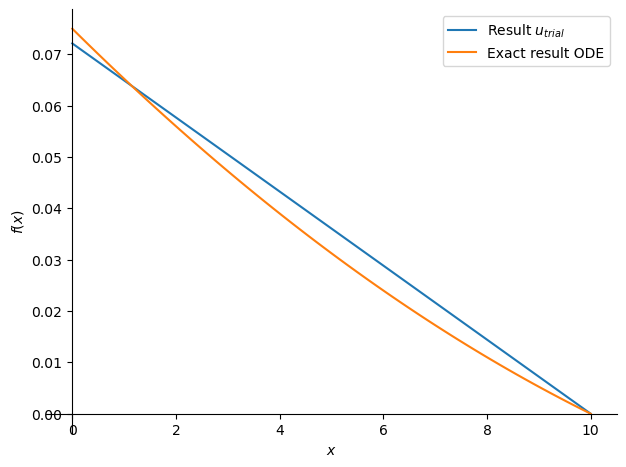
Comparison

p0 = sym.plot(u_trial_subs.subs([(F,10),(EA_0,1000),(L,10)]), (x , 0 , 10),label='Result $u_{trial}$',legend=True,show=False)
p1 = sym.plot(u_subs.subs([(F,10),(EA_0,1000),(L,10)]), (x , 0 , 10),label='Exact result ODE',show=False)
p0.append(p1[0])
p0.show()