4.1. Example System

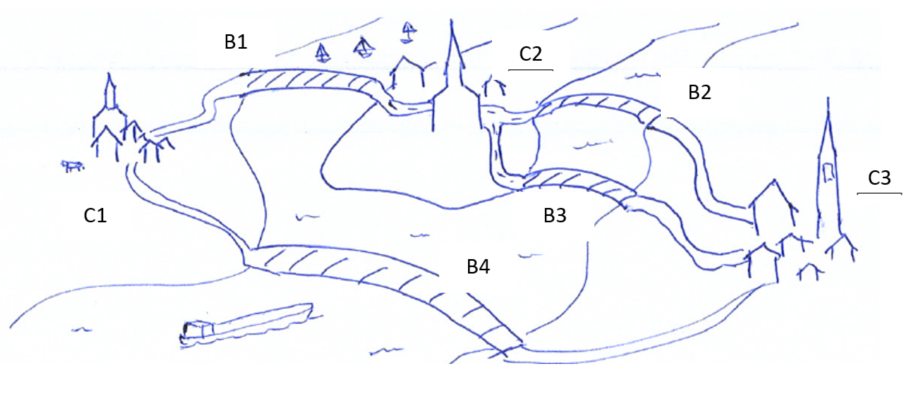
A pre-fabricated bridge design is being considered for river crossings in a remote region of the world, as shown in Figure 1. Cities 1, 2 and 3 are labelled C1, C2 and C3, with bridges labelled B1-B4.

Question 1: If the probability of failure for an individual bridge is 0.1 per year, compute the probability that you cannot drive from City 1 to City 2

Answer

\[ P_{f_{C1-C2}} = P_{f_{B1}} * P_{f_{B4-B3-B2}} = P_{f_{B1}} * (1 - (1 - P_{f_{B4}})(1 - P_{f_{B3}}*P_{f_{B2}})) \]

\[ P_{f_{C1 - C2}} = 0.1 * (1 - (1 - 0.1)(1 - 0.1 * 0.1)) = 0.0109 \]

Question 2: If the probability of failure for an individual bridge is 0.1 per year, compute the probability that you cannot drive from City 2 to City 3.

Answer

\[ P_{f_{C2 - C3}} = P_{f_{B3}} * P_{f_{B2}} * P_{f_{B1 - B4}} = P_{f_{B3}} * P_{f_{B2}} * (1 - (1 - P_{f_{B1}})(1 - P_{f_{B4}})) \]

\[ P_{f_{C2 - C3}} = 0.1 * 0.1 * (1 - (1 - 0.1)(1 - 0.1)) = 0.0019 \]

Question 3: If the probability of failure for an individual bridge is 0.1 per year, compute the probability that you cannot drive from City 1 to City 3

Answer

\[ P_{f_{C1 - C3}} = P_{f_{B4}} * P_{f_{B1-B3-B2}} = P_{f_{B4}} * (1 - (1 - P_{f_{B1}})(1 - P_{f_{B3}}*P_{f_{B2}})) \]

\[ P_{f_{C1 - C3}} = 0.1 * (1 - (1 - 0.1)(1 - 0.1 * 0*1)) = 0.0109 \]

Question 4: Suppose there is a critical facility (e.g., a hospital) in City 3. How many bridges would you need to install between City 2 and 3 to ensure that the probability of someone not reaching City 3 from City 2 is less than \(10^{-4}\)?

Answer

\[ P_{f_{C2 - C3}} = P_{f_B}^n * (1 - (1 - P_{f_{B1}})(1 - P4)) \]

\[ 0.0001 = 0.1^n * (1 - (1 - 0.1)(1 - 0.1)) \]

\[ n = 3.3 \]

It is necessary to install 2 more bridges between City 2 and 3.

Question 5: If you had 1 extra bridge to place, which bridge (i.e., B1, 2, 3 or 4) would you place it next to in order to have the biggest decrease of the probability of not reaching City 3 from City 1?

Answer

I would locate the extra bridge next to Bridge 4. In this case, adding an extra element in the parallel system, making it more redundant.

• \(P_f\) next to B1 = 0.00199

• \(P_f\) next to B2 or B3 = 0.0101

• \(P_f\) next to B4 = 0.00109

Question 6: If you only had 3 available bridges, which of the 4 bridges in the figure would you remove first, to cause the smallest reduction in failure probability?

Answer

I would remove Bridge 2 or 3. If bridge 1 or 4 is removed, a whole path is removed from the system, while by removing only Bridge 2 or 3, there is still an available bridge to cross that river.

Question 7: What should the probability of each bridge be in order to make the probability of not crossing from C1 to C3 less than 0.01?

Answer

\[ P_{f_{C1-C3}} = P_{f_{B4}} * P_{f_{B1-B3-B2}} = P_{f_{B4}} * (1 - (1 - P_{f_{B1}})(1 - P_{f_{B3}} * P_{f_B2})) \]

\[ 0.01 = X * (1 - (1 - X)(1 - X * X)) \]

\[ X = 0.0960 \]

Since the bridges have identical designs and have all been manufactured by the same contractor, positive dependence is expected between performance of bridges B1-B4.

Question 8: State whether or not dependence would increase or decrease the probability calculated in question 3, and explain why with 1 or 2 sentences.

Answer

Increase.

The probability of failure would increase because the system mainly works like a parallel system. In this case, when there is full dependence between the elements, the probability of failure equals the probability of failure of the strongest element. For instance, \(P_{f_{\text{bridges 2, 3}}}=0.01\) for independent case and 0.1 for full dependence case.

Assume each prefabricated bridge is made up of a single road deck and 5 separate frames that are joined together. Each bridge will fail if either the road deck fails, or 1 of the frames fails.

Question 9: If the probability of a frame failure is 0.01, what is the required failure probability of the road deck to make sure the bridge failure probability is no more than 0.1?

Answer

\[ P_f = 1 - (1 - P_{f_{text{deck}}})(1 - P_{f_{\text{one of the frames}}}) \]

\[ P_f = 1 - (1 - P_{f_{text{deck}}})(1 - (1 - (1 - P_{f_{\text{frame}}})^5)) \]

\[ 0.1 = 1 - (1 - P_{f_{text{deck}}})(1 - (1 - (1 - 0.01)^5)) \]

\[ P_{f_{\text{deck}}} = 0.0536 \]